Глава 1. Установка системы и начало работы с ней

1.1. Краткая характеристика системы

1.1.1. Maple V — лидер среди систем символьной математики

Известно, что на защитах диссертации нередко встречаются две крайности. Ученые мужи часто обвиняют соискателей в отсутствии серьезных расчетов на компьютерах. А если они и приводятся, то выдвигается встречное обвинение — отсутствие серьезной аналитической обработки математических данных. При этом имеются в виду вполне справедливые доводы — численные расчеты всегда носят частный характер, а отсутствие простых аналитических методов расчета препятствует разработке научно обоснованных инженерных методик проектирования различных изделий и позволяет усомниться в достоверности расчетов.

Между тем вряд ли правильно требовать глубоких математических знаний от специалистов в области прикладных наук, равно как и требовать таких знаний в этих науках от математиков-теоретиков и аналитиков. Афоризм, приписываемый Кузьме Пруткову, о том, что «нельзя объять необъятное» тут более чем уместен. Вот почему и те и другие остро нуждаются в высококлассных системах компьютерной алгебры, вобравших в себя достижения многих математических школ за сотни лет их развития и способных решать математические задачи в аналитическом виде.

Специалисты в прикладных науках могут легко переложить на них свои заботы по доведению аналитических преобразований до нужного им уровня и избавиться от частого привлечения к своим проектам плохо понимающих их сущность математиков-теоретиков. Последние в свою очередь избавляются от рутинной и малоинтересной работы в области прикладных расчетов и могут сосредоточиться на решении в общем виде действительно фундаментальных математических проблем — в том числе и направленных на дальнейшее совершенствование систем компьютерной алгебры и разработку методик применения таких систем для решения серьезных математических задач.

Maple V — система компьютерной алгебры, рассчитанная на серьезного пользователя. Казалось бы, нелепо называть ее математической системой «для всех». Однако по мере распространения этой системы (и даже знакомства с ней) она становятся полезной для многих пользователей ПК, вынужденных в силу обстоятельств (работа, учеба, хобби) заниматься математическими вычислениями. Для большинства из них (в том числе и для профессионалов-математиков) возможности систем символьной математики, реализованных на массовых ПК класса IBM PC AT, являются полной неожиданностью и вызывают вполне оправданное удивление и восхищение, а порою и резкое отрицание. Впрочем, последнее характерно для тех, кто с системой Maple V просто не работал!

Maple V изумительно продуманная система. Она с равным успехом может использоваться как для простых, так и самых сложных вычислений. Заслуженной

Краткая характеристика системы 13

популярностью система пользуется в университетах — свыше 300 самых крупных университетов мира (включая и наш МГУ) взяли эту систему на вооружение. А число только зарегистрированных пользователей системы превысило I млн. Любопытно отметить, что у популярной математической системы MathCAD число зарегистрированных пользователей около 600 тыс., т. е. меньше, чем у Maple V! Система Maple V особенно популярна в университетах — свыше 300 ведущих университетов мира (включая наш МГУ) применяют эту систему в учебе и в научных исследованиях.

Добавьте к этому куда большее число незарегистрированных пользователей — ведь система Maple V R4 вполне легально выставлена для копирования на Internet-узле фирмы Waterloo Maple (см. главу 14) и записана на многих CD-ROM. Если учесть все это, то оказывается, что популярность системы Maple V ничуть не ниже, а то и выше популярности гораздо более простых систем (а по сравнению с Maple даже ущербных) — таких, как Derive и MathCAD. Вот и решайте, какая из систем действительно рассчитана на всех!

Maple V — типичная интегрированная система. Это означает, что она объединяет в себе ориентированный на сложные математические расчеты мощный язык программирования (и он же входной язык для интерактивного общения с системой), редактор для подготовки и редактирования документов и программ, математически ориентированный входной язык общения и язык программирования, современный многооконный пользовательский интерфейс с возможностью работы в диалоговом режиме, справочную систему, ядро алгоритмов и правил преобразования математических выражений, программные численный и символьный процессоры с системой диагностики, мощнейшие библиотеки встроенных и дополнительных функций, пакеты расширений и применений системы и огромную и очень удобную в применении справочную систему. Ко всем этим средствам имеется полный доступ прямо из системы.

Maple V — одна из самых мощных и «разумных» интегрированных систем символьной математики, созданная фирмой Waterloo Maple Inc. (Канада). Эта система на сегодня является лучшей математической системой компьютерной алгебры для персональных компьютеров, имеющей большое число встроенных функций, обширные библиотеки расширения и богатейшие графические возможности, с блеском решающие задачи наглядной визуализации сложнейших математических расчетов.

Во многих обзорах систем компьютерной алгебры Maple V справедливо считается одним из первых кандидатов на роль лидера среди таких систем, ориентированных на серьезное применение. Это лидерство она защищает в честной конкурентной борьбе с другой замечательной математической системой — Mathematica 2 (а сейчас и Mathematica 3). Каждая из этих систем имеет свои особенности, но в целом эти две лидирующие системы поистине «два сапога пара».

Система Maple V прошла долгий путь развития и апробации. Она реализована на больших ЭВМ, рабочих станциях Sun, ПК, работающих с операционной системой Unix, ПК класса IBM PC, Macintosh и др. Все это самым положительным образом повлияло на ее отработанность и надежность (в смысле высокой вероятности правильности решений и отсутствия сбоев в работе). По этому показателю Maple V заметно превзошла своего ближайшего и очень серьезного конкурента — систему Mathematica 2 и 3, несколько превосходящую Maple V по специальным видам графики.

14 Установка системы и начало работы с ней

Для пользователей (особенно наших) немаловажно то обстоятельство, что Mat-hematica 2 имеет систему защиты от несанкционированного использования и копирования, тогда как поставляемая на ряде CD-ROM и по сети Internet Maple V R4 — полностью открытая для применения система. От поставляемых на рынок серийных и платных систем она отличается лишь отсутствием документации, которую во многом заменяет данная книга.

Кроме того, если не считать начальных усилий по освоению системы. Maple V вполне можно использовать без отдельной документации, тогда как с применением систем Mathematica 2 и 3 этот номер не проходит. Впрочем, объективности ради надо отметить, что в новейшей версии Mathematica 3 под Windows многие из недостатков устранены, пользовательский интерфейс заметно улучшен, а графические возможности, пожалуй, даже превосходят таковые для системы Maple V. Однако из-за проблем защиты от копирования и разбухания системы Mathematica до 120 Мбайт эта система пока еще используется у нас редко.

Maple V в настоящее время выпускается в ряде версий, называемых реализация-ми. Основной и самой известной является реализация Maple V R4 Power Edition. На Западе ей на смену приходит новейшая реализация R5, хотя коммерческий выпуск реализации R4 с документацией продолжается. Обе реализации по математическим возможностям мало чем отличаются друг от друга — в реализации R5 появилась возможность работы с электронными таблицами, несколько улучшен интерфейс пользователя (введены палитры для ввода математических символов и расширены возможности управления мышью), стала возможной запись файлов в формате Internet (HTML) и введена возможность обмена объектами документов по методу «Drag and Drop» (Тяни и Отпускай). Обе реализации выпускаются в трех модификациях — полной (Power Edition), стандартной (Standard) и студенческой (Student). В данной книге в основном рассматривается самая популярная, распространенная и полная версия Maple V — Power Edition.

1.1.2. Об ошибках в символьных вычислениях

На многих пользователей системами символьной математики удручающее впечатление может произвести наличие хотя и редких, но ошибочных решений. В самом деле, мы немедленно стерли бы с жесткого диска табличный процессор, давший ошибку в бухгалтерских расчетах, или систему проверки орфографии, дающую ошибки при проверке. Впрочем, последний случай не столь уж и тривиален — пока нет таких систем, которые давали бы стопроцентную достоверность проверки орфографии и грамматики. Тот же текстовый процессор Word 95/97 сплошь и рядом спотыкается при проверке орфографии текстов, в чем автор не раз убеждался, готовя по нему большую книгу [8].

Ситуация с системами компьютерной алгебры и того хуже. Некоторые, к счастью, достаточно редкие, ошибки и неопределенности в них как бы заранее запрограммированы. К примеру, что считать более простым выражением tan(x) или sin(x) / cos(x)'> Система Derive полагает более простым выражением tan(x) и преобразует к нему выражение sin(x) / cos(x). А вот система Maple V ничуть не менее справедливо считает, что функции sin(x) и cos(x) математически более простые, чем tan(x) и вообще tan(x) по сути не самостоятельная функция, а sin(x) /cos(x). Поэтому Maple V везде вместо tan(x) будет выводить sin(x) /cos(x).

Краткая характеристика системы 15

Представьте себе, что таких недоразумений десятки и вы ничего об этом не знаете. Поэтому не стоит удивляться, что порою символьное значение какой-либо производной или интеграла заметно отличается по виду от приводимого в том справочнике, из которого взято исходное выражение для проверки системы. Обычно требуются определенные усилия для доводки результата вычислений, либо конкретные указания системе о типе преобразований в ходе вычислений. Они реализуются в виде опций к командам и функциям системы.

По образному выражению автора обзора [40], решение задач в символьном виде напоминает переход через минное поле, густо напичканное минами. Удивительно не то, что системы символьной математики могут ошибаться и «взрываться», а то, что число этих ошибок мало и уже на нынешнем этапе развития таких систем это не мешает серьезному практическому применению их. Еще раз подчеркнем, что Maple V в этом отношении является одной из лучших систем, практически реализованных на ПК класса IBM PC и Macintosh, с достаточно умеренными техническими характеристиками. Кстати говоря, для ПК Macintosh пока последней реализацией является Maple V R4.

Иногда можно услышать, что компьютеры делают умных людей умнее, а глупых — глупее. Пожалуй, это более чем справедливо для людей, сидящих у ПК с установленной на нем системой символьной математики. Лишь те, кто понимают суть математических вычислений и имеют должную математическую интуицию и подготовку, могут получить от таких систем самые серьезные и даже новые результаты. Те же, кто думает, что системы символьной математики заменят им математические знания, глубоко ошибаются и могут получить красочно выглядящие, но абсолютно неверные и даже псевдонаучные результаты!

Однако вряд ли следует переоценивать вероятность выдачи системами символьной математики ошибочных результатов — даже самые опытные математики-аналитики тоже могут ошибаться в своих вычислениях. В разработке таких систем, как Maple V R4/R5 или Mathematica 2/3, принимают участие крупные математические школы всего мира! Эти системы подлинный кладезь математических понятий, сведений и знаний. Они способны заменить самые серьезные справочники по математическим вычислениям в любой области науки, техники и образования. Кроме того, они имеют множество средств для проверки корректности выполняемых вычислений, например, подстановку полученных результатов в исходные выражения.

Кстати, одно из самых действенных приемов проверки таких средств — решение задачи одновременно на нескольких системах символьной математики. Не случайно уже сейчас можно заметить тенденцию к объединению математических систем. Эта новая и безусловно прогрессивная тенденция в ближайшее время приведет к созданию автоматизированных рабочих мест математиков и ученых других специальностей. Разработки таких рабочих мест (разумеется, компьютерных), в том числе с использованием систем Maple V, уже появились, и о них немного говорится в Заключении к этой книге.

1.1.3. Вызов функций пакетов расширения Maple V

Основой символьной мощи Maple V является ядро системы. Оно содержит сотни базовых функций и алгоритмов символьных преобразований. В новых реализаци-ях объем ядра достигает 6-7 Мбайт. Имеется также основная библиотека операторов, команд и функций. Многие встроенные в нее функции, как и функции ядра.

16 Установка системы и начало работы с ней

могут использоваться без какого-либо объявления, другие нуждаются в объявлении. Кроме того, имеется ряд пакетов расширения системы (packages).

Дополнительные функции из пакетов расширения должны применяться после объявления загрузки пакета с помощью слова

with(name)

где name — имя применяемого пакета. С учетом встроенных в ядро функций и функций пакетов расширения их общее число в системе Maple V R3 приближается к 2500, а в реализации R5 к 2700. Это означает, что великое множество задач может решаться в режиме прямого диалога с системой без использования каких-либо средств программирования.

1.1.4. Языки системы — входной, реализации и программирования

Maple V предназначена для решения огромного числа задач вообще без какого-либо их программирования в общепринятом смысле этого понятия. Достаточно лишь описать алгоритм задачи и разбить его на вопросы, на которые система Maple V способна дать ответы. Более того, есть тысячи задач, алгоритмы решения которых уже реализованы функциями и командами системы. Тем не менее это вовсе не означает, что система Maple V не относится к системам программирования. Более того, на самом деле эта мощная современная система программирования основана на трех языках — входном, реализации и программирования.

Maple V имеет входной язык сверхвысокого уровня, ориентированный на решение математических задач практически любой сложности. Он служит для задания системе вопросов или, говоря иначе, задания входных данных для последующей их обработки. Это язык интерпретирующего типа и по идеологии работы с ним напоминает добрый старый Бейсик. И такое сходство вовсе не недостаток, а огромное достоинство — ведь именно с Бейсика начался подлинный диалог пользователя напрямую с компьютером! Входной язык имеет большое число заранее определенных математических и графических функций, а также обширную библиотеку расширения системы.

Имеет Maple V и свой язык процедурного программирования — Maple-язык. Этот язык, будучи частью входного языка, имеет вполне традиционные средства для подготовки на основе принципов структурного подхода типовых задач программирования: циклы, условные и безусловные переходы, операторы сравнения, логические операторы, команды управления внешними устройствами, функции пользователя, процедуры и т.д. Но, помимо этих возможностей, языку Maple V доступны все специальные операторы и функции, которыми располагает система. Многие из них заменяют весьма серьезные программы — например, символьного дифференцирования, интегрирования, разложения в ряд Тейлора, построения сложных трехмерных графиков и т.д.

Не следует путать входной язык и язык программирования системы (словом Maple-язык) с языком ее реализации. Им является один из самых лучших и мощных универсальных языков программирования — С (Си). На его основе подготовлено ядро системы, содержащее тщательно оптимизированные процедуры. Большинство же функций системы — библиотечные из пакетов расширения, поставляемых с системой. Они подготовлены на Maple-языке программирования системы, могут дополняться и даже модифицироваться. По разным оценкам лишь

Краткая характеристика системы 17

от 5 до 10 процентов средств Maple V создано на языке реализации — все остальное написано на Maple-языке программирования системы. Таким образом, система имеет развитые возможности к расширению и адаптации к задачам пользователя.

Для подготовки программ на языке системы могут использоваться внешние редакторы, но система Maple V имеет и свой встроенный редактор, вполне удовлетворяющий большинство пользователей. Он и вводится командами в позиции Edit главного меню. Этот редактор можно использовать для редактирования программных файлов или математических выражений. Версии Maple V под MS-DOS снабжены своим редактором программ и отладчиком с функциями синтаксического контроля. В версиях Maple V под Windows необходимость в этих средствах практически отпала.

Язык программирования Maple V напоминает (в части основных средств) смесь Бейсика и Паскаля. Это облегчает знакомство с ним для тех, кто имеет хотя бы умеренный опыт программирования на этих языках. По близким к Бейсику правилам (и общепринятым математическим сокращениям) выполняется и ввод математических выражений в диалоговом режиме работы с системой.

1.1.5. Пользовательский интерфейс

Долгое время Maple V имел довольно архаичный (хотя и неплохой) пользовательский интерфейс, ориентированный на операционную систему MS-DOS. Но затем версия Maple V R3, затем Maple V R4 и, наконец, Maple V R5, приобрели вполне современный графический пользовательский интерфейс, характерный для приложений под операционные системы Windows 3.1/3.11/95. Это намного повысило удобство работы с системой и обеспечило простую интеграцию со многими другими программными продуктами.

Пользовательский интерфейс Maple V R4 позволяет готовить документы в стиле Notebook (Блокнот), содержащие одновременно текстовые комментарии, задания в виде функций в командной строке (с возможным преобразованием их в естественную математическую форму), результаты вычислений в виде обычных математических формул и графические данные. Это обеспечивает высокую степень визуализации как исходных данных, так и результатов вычислений.

В основе пользовательского интерфейса Maple V R4 лежит графический интерфейс операционной системы Windows 3.1/3.11 или Windows 95. Интерфейс Maple V R4 является многооконным. Управление системой возможно с помощью главного меню, панелей с кнопками быстрого управления и «горячими» клавишами. Реализуются многие возможности графического манипулятора — мыши, пожалуй, за исключением метода перетаскивания мышью объектов.

Важно отметить и прекрасно выполненную справочную систему Maple V R4. Преодолев первые трудности общения с системой, пользователь быстро осваивает систему помощи, которая позволяет без какой-либо документации получить исчерпывающую информацию о любом операторе, функции или пакете применения системы (разумеется, на английском языке). В каждую справку входит по несколько примеров применения, причем их можно скопировать и перенести в редактор или в окно исполняемых документов системы. Это способствует быстрому обучению пользователя.

18 Установка системы и начало работы с ней

Пользователь (как и в ряде других математических систем) работает с документами, которые являются одновременно описаниями алгоритмов решения задач, программами и результатами их исполнения. Они размещаются в соответствующих ячейках.

Графические построения выполняются как в ячейках документа, так и в отдельных окнах, и имеют свои меню для оперативного управления параметрами графики.

1.1.6. Ориентация системы Maple V

Вообще говоря, система Maple V ориентирована на решение сложных задач, хотя и решение в ней простых задач вполне возможно и уместно. Для решения таких задач вполне подойдет весьма простая, быстрая и надежная система Derive или система MathCAD, в которую (начиная с версии 3.0 под Windows) включен приобретенный по лицензии фирмы Waterloo Maple упрощенный символьный процессор Maple. Однако по числу доступных пользователю математических функций эти скромные системы не идут ни в какое сравнение с патриархом символьной математики Maple V.

Перечислим основные возможности системы Maple V R4.

Возможности интерфейса

• работа со многими окнами;

• вывод графиков в отдельных окнах или в окнах документа;

• представление выходных и входных данных в виде естественных математических формул;

• задание текстовых комментариев различными шрифтами;

• возможность использования гиперссылок и подготовки электронных документов;

• удобное управление с клавиатуры, с помощью главного меню и инструментальной панели;

• управление с помощью графического манипулятора — мыши.

Символьные и численные вычисления

• дифференцирование функций;

• численное и аналитическое интегрирование;

• вычисление пределов функций;

• разложение функций в ряды;

• вычисление сумм и произведений;

• интегральные преобразования Лапласа, Фурье и др.;

•дискретные Z-преобразования;

• прямое и обратное быстрое преобразование Фурье;

• работа с кусочными функциями.

Численное и символьное решение уравнений

• решение линейных и нелинейных систем уравнений;

• решение систем дифференциальных уравнений;

• символьное вычисление рядов;

• работа с рекуррентными функциями;

• решение трансцендентных уравнений;

• решение систем с неравенствами.

Краткая характеристика системы 19

Вычисление элементарных и специальных математических функций

• вычисление всех элементарных функций;

• вычисление большинства специальных математических функций;

• пересчет координат точек для множества координатных систем;

• задание произвольных функций пользователя.

Линейная алгебра

» свыше 100 операций с векторами и матрицами;

• решение систем линейных уравнений;

• формирование специальных матриц и их преобразования;

• вычисление собственных значений и собственных векторов матриц.

Графическая визуализация вычислений

• построение графиков многих функций;

• различные типы осей (с линейным и логарифмическим масштабом);

• графики функций в Декартовой и в полярной системах координат;

• специальные виды графиков (точки массивов, векторные, диаграммы уровней и др.);

• системы координат, определяемые пользователем;

• графики, представляющие решения дифференциальных уравнений;

• графики трехмерных ЗО-поверхностей с функциональной закраской;

• построение пересекающихся в пространстве объектов;

• задание пользователем окраски графиков;

• импорт графиков из других пакетов и программных систем;

• задание анимационных графиков;

• проигрывание анимационных файлов с помощью специального проигрывателя.

Программирование

• мощный встроенный язык процедурного программирования;

• простой и типичный синтаксис языка программирования;

• обширный набор математических типов данных;

• типы данных, задаваемых пользователем;

• средства отладки программ;

» мощные библиотеки расширения языка программирования;

• задание внешних функций и процедур;

• программный интерфейс с языками программирования С, Fortran и LaTeX.

Система Maple V R4 может применяться для решения самых серьезных математических задач аэродинамики, теории поля, теплопроводности и диффузии, теоретической механики и др. Проекты с такими задачами нередко являются многолетним трудом элитных научных коллективов.

Впрочем, коль система установлена на массовом ПК, ее можно (да и нужно) применять как можно чаще и по любому поводу. Это способствует практическому освоению и более эффективному применению системы — равно как и росту математических познаний тех, кто с ней работает.

20 Установка системы и начало работы с ней

1.2. Загрузка системы Maple V R4 и ее состав 1.2.1. Аппаратные требования и инсталляция

В этой книге в основном рассматривается реализация системы — Maple V R4, ориентированная на наиболее распространенные у нас ПК класса IBM PC AT, построенные на базе микропроцессоров 386/486/Pentium/Pentium ММХ/Реп-tium Pro/Pentium II, имеющих ОЗУ не менее 8 Мбайт. Для современных ПК это уже небольшая память, так что можно считать, что аппетиты Maple V на память ПК и их аппаратные ресурсы достаточно умеренны. Хотя, увеличение памяти до 16 и более Мбайт делает работу с системой явно более резкой, чем при минимальном объеме памяти.

На жестком диске система занимает от 16 до 30 Мбайт (конкретный объем зависит в основном от размера поставляемых вместе с системой библиотек — в частности, библиотеки совместного использования пользователями SHARE). Стоимость системы около 700 долл. (США). Документация по Maple V R4 — две большие книги (37, 38]. К сожалению, она крайне дефицитна. Тем не менее фирма Maple позаботилась о том, чтобы системой могли пользоваться все, а не только счастливые владельцы указанных книг. Это достигнуто введением в систему мощной справочной базы данных с огромным числом примеров.

Для установки Maple V R4 Вы должны иметь ПК с указанной выше конфигурацией. Система располагается (в частично упакованном виде) на 5 дискетах 1.44 Мбайт. Инсталляция системы проходит гладко и не требует пояснения. При инсталляции в самой массовой операционной системе Windows 95 в рабочем меню появляется подменю со значками Maple V (в некоторых поставках на рабочем столе появляется ярлык-ускоритель с изображением кленового листка и надписью Maple V R4). С системой поставляется ее версия под MS-DOS, редактор и корректор для файлов документов, архиватор библиотечных файлов и другие вспомогательные утилиты.

1.2.2. Запуск системы

Запуск системы производится указанием на ярлык-ускоритель (или соответствующую позицию в меню программ) курсором мыши и быстрым двойным нажатием левой ее клавиши. При этом на некоторое время появляется красочное окно-заставка системы, а затем основное окно системы (рис. 1.1).

Проблемы, связанные с инсталляцией и возможными конфликтами, описаны в файле readme, который рекомендуется просмотреть перед инсталляцией системы. К сожалению, он подготовлен на английском языке, как и вся встроенная в Maple V документация.

1.3. Работа в диалоговом режиме

1.3.1. Начальные навыки работы

После загрузки и пуска системы можно начать диалог с ней, используя ее операторы и функции (с параметрами) для создания и вычисления математических выражений. На рис. 1.2 представлен реальный диалог с системой (в виде прямой копии с экрана) при решении простейших арифметических задач.

Работа в диалоговом режиме 21

Рис. 1.1. Начальный момент запуска системы Maple V R4.

Уже из этого простого примера видны особенности диалога с системой и синтаксиса ее входного языка — т. е. языка задания системе вопросов. Диалог идет в стиле: задал вопрос — получил ответ. Вопросы и ответы занимают отдельные блоки, выделяемые в левой части квадратными скобками. Длина квадратных скобок зависит от размера выражений — исходных (вопроса) и результатов вычислений (ответов на вопросы). Знак > является знаком приглашения к заданию вопроса. Мигающая вертикальная черта ¦ — маркер ввода.

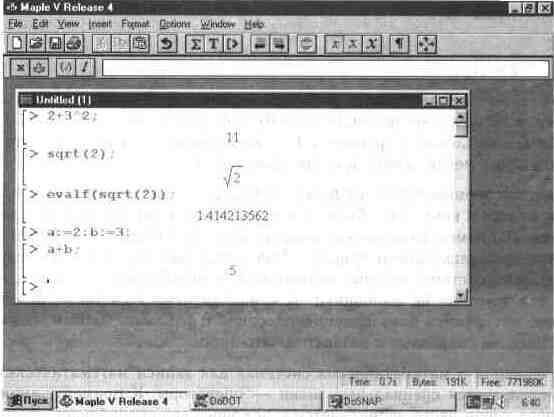
Рис. 1.2. Начало диалога с системой Maple V R4.

it установка системы и начало работы с ней

Ввод выражений (вопросов) задается по правилам, издавно принятым для строчных редакторов. Они общеизвестны, и подробно на них останавливаться не стоит. Отметим лишь, что клавиша Ins позволяет задавать два основных режима ввода — замены и вставки. В режиме замены вводимый символ заменяет существующий, который отмечен маркером ввода. А в режиме вставки новый символ вводится в текст, не уничтожая имеющиеся символы.

Перемещение маркера ввода осуществляется (клавишами <— и —> перемещения курсора. Клавиша стирания с символом <—— стирает символ слева от маркера ввода, а клавиша Del — справа от него. Для ввода любого символа надо нажать соответствующую клавишу клавишного пульта. Клавиша Shift включает верхний регистр для ввода больших (заглавных) букв, а клавиша Caps Look переключает верхний и нижний регистры (они меняются местами).

Знак фиксации конца выражения ; (точка с запятой) указывает, что результат его вычисления должен быть выведен на экран дисплея, а знак : (двоеточие) отменяет вывод и может использоваться как знак разделителя при записи в одной строке нескольких выражений. Клавиши перемещения курсора позволяют пробежаться по ранее введенным строкам сеанса (сессии) работы.

1.3.2. Понятие функции и оператора

Важным понятием системы Maple V (да и математики вообще) является понятие функции. Функция в выражениях вводится заданием ее имени и списка из одного или ряда параметров в круглых скобках, например, sqrt(2) задает функцию — вычисление квадратного корня с параметром 2 (численной константой). Основным признаком функции является возврат ею значения в ответ на обращение к функции по ее имени — идентификатору с указанием списка параметров функции. Например:

>2'sin(1.);

1.682941970

>2'sin(1);

2sin(1)

Обратите внимание на особую роль здесь десятичной точки — она служит указанием о вычислении значения sin(l.O) или, что то же самое, sin(l.). А вот синус для целочисленного аргумента 1 не вычисляется — считается, что вычисленное значение менее ценно, чем значение sin(l).

Ради единства терминологии мы будем пользоваться расширительным понятием функции, относя к нему и те объекты, которые иногда именуют процедурами или командами. Например, графические объекты plot и plot3d мы также будем считать функциями, возвращающими графики. Под командами мы будем подразумевать такие указания системе, которые готовят ее к определенным действиям, но сами по .себе эти действия не выполняют. К командам относятся также действия по изменению интерфейса и выполнению операций с файлами. Словом, команды — это действия, не связанные с возвратом чего-либо.

Помимо функций в математических системах для записи математических выражений используется специальные знаки — операторы. К примеру, вычисление квадратного корня часто записывается с помощью его специального знака — ^1. Достаточно хорошо известны такие операторы, как операторы сложения + ,

Работа в диалоговом режиме 23

вычитания - , умножения * , деления / и некоторые другие. Операторы обычно используются с операндами в виде констант или переменных, например, в записи 2*(3+4) числа 2, 3 и 4 — это операнды, а знаки * и + — операторы. Скобки используются для изменения порядка выполнения операций. Так, без них выражение 2*3+4=10, тогда как 2*(3+4)=14, поскольку вначале вычисляется выражение в скобках.

Пожалуй, самым распространенным оператором является оператор присваивания :=. Он используется для задания переменным конкретных значений, например:

х:=у y:=z z:=2

> х:=у;

> y:=z;

> z:=2;

> х;

>^

2 2

Этот простой пример наглядно иллюстрирует эволюцию переменных и особую роль оператора присваивания в системе Maple V. В частности, в этом примере переменные х, у и z взаимосвязаны с помощью операций присваивания. Поэтому задание значения числа 2 последней переменной приводит к тому, что и переменные у и х принимают то же значение.

Другой распространенный оператор равенства = используется для задания равенств и логических условий (например, а=Ь), указания областей изменения переменных (например, i=1..5 означает формирование изменения i от 1 до 5) и значений параметров — опций в функциях и командах (например, color=black для задания черного цвета у линий графиков).

Операторы сами по себе результат не возвращают. Но они, наряду с функциями и своими параметрами — операндами, позволяют конструировать математические выражения, которые при их вычислении также возвращают результат. В силу этого математические выражения, содержащие операторы и операнды, могут быть параметрами функций. Выражения в Maple V бывают очень простыми (например, имена переменных х и у или константы 1 или 2), а могут содержать многие тысячи знаков.

С позиции символьной математики квадратный корень из двух уже является основным результатом вычислений, поэтому такая функция обычно не вычисляется в численном виде, а выводится в естественном виде — с применением знака квадратного корня ^/. Для вычисления в привычном виде (десятичного числа с мантиссой и порядком) надо воспользоваться функцией evalf(sqrt(2)) — эта функция обеспечивает эволюцию (в нашем случае просто вычисление) символьного выражения, заданного ее параметром (числом 2).

Более подробно тонкости входного языка общения с системой и языка ее программирования описаны в главе 9.

24

Установка системы и начало работы с ней

1.3.3. Управление окном документа

Пока мы вели вычисления в открывшемся окне редактирования с именем Untitled (1). Как любое окно в системе Windows 95, оно имеет титульную строку с тремя кнопочками в конце ее: для сворачивания окна, переключения в полное или частичное открытие окна и для закрытия окна (в последнем случае вся информация в окне теряется и окно исчезает). Кроме того, окно можно перемещать, уцепившись курсором мыши за свободное поле титульной строки и удерживая нажатой левую клавишу мыши. Наконец, окно можно растягивать в разные стороны, цепляясь курсором мыши за границы окна.

1.3.4. Примеры задания функции пользователя и построения ее графика

На рис. 1.3 показано продолжение наших начальных экспериментов после полного открытия окна редактирования.

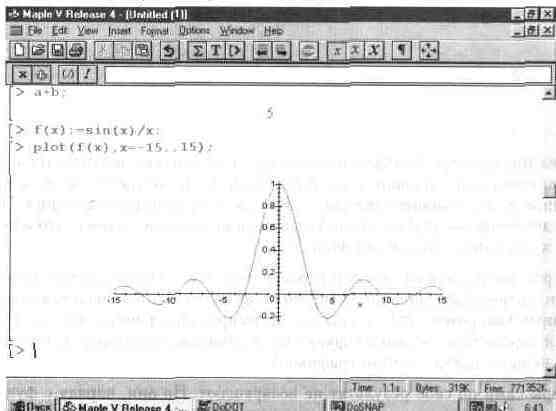
Рис. 1.3. Пример задания функции пользователя и построения ее графика.

В данном случае показано, как задается функция пользователя f(x) с одним параметром х. Нетрудно заметить, что параметр указывается в скобках после имени функции, а для записи выражения функции используется знак присваивания := (двоеточие со знаком равенства).

Для построения графика функции f(x) используется функция plot в форме:

plot(f(x),x=-15..15)

Нетрудно заметить, что при нескольких параметрах функции (в нашем случае их два) параметры указываются через запятые. Выражение х=-15..15 задает указание во-первых, относительно какой переменной строится график, а во-вторых, в какой области значений меняются значения этой переменной (в нашем случае от -15 до +15). Шаг изменения переменной задается автоматический с тем, чтобы график был достаточно представительным.

Работа в диалоговом режиме

25

1.3.5. Пример построения графика трехмерной поверхности

Столь же просто, как и график обычной функции в Декартовой системе координат, можно построить график трехмерной поверхности. Это показано на примере рис. 1.4. В данном случае задана функция двух переменных Z(x,y):=sin(x*y) и ее график строится с использованием графической функции plot3d. Правила задания пределов изменения переменных х и у соответствуют описанным выше.

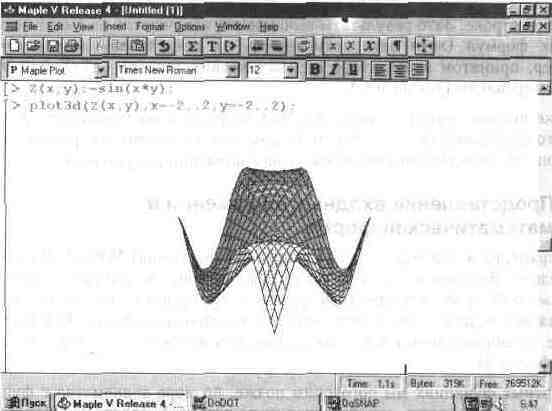
Рис. 1.4. Построение графика трехмерной поверхности.

Вероятно, многих читателей вполне удовлетворят уже описанные возможности, но сила системы Maple V R4 прежде всего в том, что она выполняет аналитические (символьные) вычисления. Поэтому покажем лишь некоторые из этих возможностей.

1.3.6. Управление формой представления документа

Приведенные выше примеры реализуют обычную форму представления документа. В нем имеются текстовые комментарии (для их ввода нажимается клавиша F5), заданные на Maple-языке задания на вычисления, результаты вычислений в виде обычных математических формул и, там где это надо, графики.

Эта выстраданная форма представления документов является компромиссом между наглядностью визуализации документа и простотой ввода исходных данных. Может показаться, что в этом отношении продвинуты системы класса MathCAD — исходные данные и описание алгоритмов вычислений у них давно задаются в виде естественных математических символов и формул, за исключением, правда, функций символьных вычислений, которые пока не имеют общепринятых специальных математических символов и вводятся именами.

Однако это кажется достоинством лишь на первый взгляд. Ввод сложных формул довольно трудоемок и требует специфических навыков, отсутствующих даже у самых опытных пользователей. В MathCAD эта проблема решена вводом панелей

26 Установка системы и начало работы с ней

(палитр) с полным набором всех математических символов и шаблонов для представления сложных формул, таких, как интегралы, суммы и произведения рядов, производные и т.д. Тем не менее, хотя их ввод при этом и становится простым, легким его не назовешь, а монотонность операции нервирует многих пользователей.

В Maple V R4 ввод исходных данных задается-привычными для языков программирования средствами — с помощью функций и операторов, записываемых в командной строке. Зато результаты вычислений получаются по умолчанию в виде обычных формул (хотя есть возможность их представления в другом виде, например, принятом в редакторе математических текстов LaTeX или у языков программирования Fortran и С).

И все же вид документа с таким заданием формул может озадачить математика и любого пользователя, не очень-то знакомого с основами программирования. В целом он отрицательно сказывается на визуализации документов.

1.3.7. Представление входных выражений в математической форме

Для устранения этого недостатка (а скорее противоречия) Maple V R4 предлагает ряд средств. Во-первых, это текстовые комментарии, в которые можно вводить формулы. Во-вторых, это инертные функции, которые не вычисляются, но дают вывод на экран дисплея в естественной математической форме. И в-третьих, это быстрое преобразование строковых выражений ввода в естественные математические формулы.

Об инертных функциях мы поговорим позже, по мере знакомства с функциями, а пока остановимся на преобразовании выражений ввода на Maple-языке в обычные математические формулы. Для этого достаточно при установленном на входном выражении маркере мыши активизировать первую клавишу панели форматирования входных выражений — соответствующее выражение тут же приобретает вид обычной математической формулы (рис. 1.5), показывающий назначение элементов панели форматирования и пример преобразования функции интегрирования в обычное представление интеграла.

Таким образом, всегда можно получить формульное представление входных выражений. Более того, другой кнопкой их можно превратить в инертную форму, когда выражение перестает вычисляться и становится, по существу, обычным комментарием.

Заметим, что пока формула является входным выражением в активной форме, она может редактироваться, но не сама по себе, а в виде текстового выражения, имеющегося в поле редактирования панели форматирования. При этом изменение записи выражения в поле редактирования немедленно влечет соответствующее изменение вводимой формулы. Это тоже довольно удобное средство, имеющее свои преимущества перед прямым редактированием формулы — в MathCAD, например, прямое редактирование формул требует определенных навыков и усваивается довольно трудно.

Следует, однако, учитывать, что представление входных выражений в виде формул обычно занимает заметно больше места в документе, чем описание выражения на Maple-языке, поэтому оно используется довольно редко. Кроме того, далеко не всякое входное выражение может быть представлено в виде

Примеры символьных вычислений

27

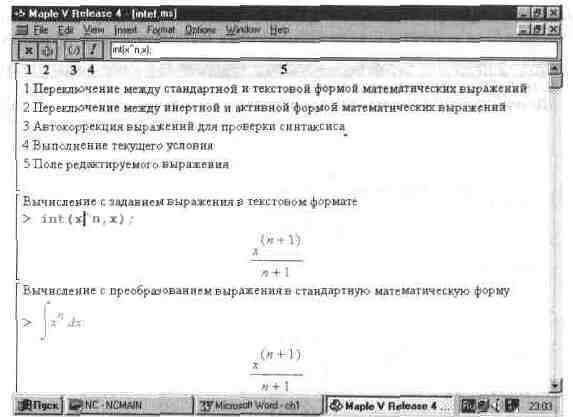
Рис. 1.5. Назначение элементов панели форматирования входнв1х выражении и их представление в виде обычных математических формул.

математической формулы — многие функции ядра, основной библиотеки и расширений Maple V попросту не имеют общепринятых обозначений в виде специальных математических знаков.

1.3.8. Управление от мыши

Для управления состоянием ячеек можно использовать контекстно-зависимое меню, появляющееся при нажатии правой клавиши мыши. Если маркер ввода установлен во входной ячейке, то это меню имеет три позиции:

Standart Math	Включает и выключает показ входных выражении в естественниц математической форме.
Maple Input	Управляет статусом (текст/ввод) ячейки ввода.
Evalution	Включает исполнение (эволюцию) ячейки. "

Левая клавиша мыши может использоваться для активизации и расширения выделения выражений в строке ввода или полного ее выделения.

К сожалению, роль управления мышью в реализациях R3 и R4 принижена. Такие возможности, как работа с контекстно-зависимым меню правой клавиши мыши и перетаскивание с ее помощью объектов с одного места на другое, реализованы только в новейшей реализации системы Maple V R5. Они описаны в главе 14.

1.4. Примеры символьных вычислений

На рис. 1.6 показано несколько примеров выполнения символьных вычислений:

преобразование тригонометрического выражения с помощью функции упрощения Simplify, вычисление суммы ряда функцией Sum и вычисление неопределенного

28

Установка системы и начало работы с ней

интеграла функцией int. Кстати, на примере вычисления суммы видно, что Maple может выдавать результаты в виде специальных математических функций.

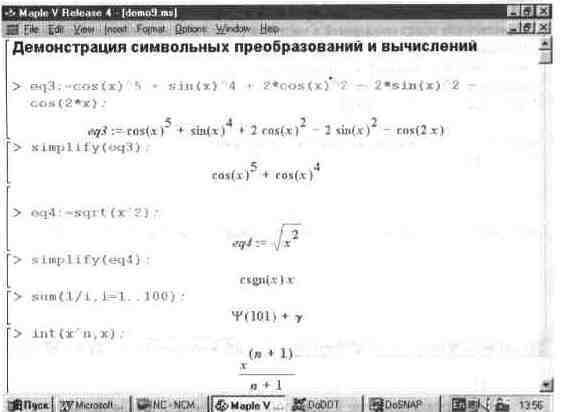
Рис. 1.6. Примеры символьных вычислении.

Вычисления в символьном виде производных и интегралов, пожалуй, являются наиболее характерными областями применения систем символьной математики. На рис. 1.7 показаны примеры таких вычислений с применением функции сИГдля вычисления производной и int для вычисления интегралов.

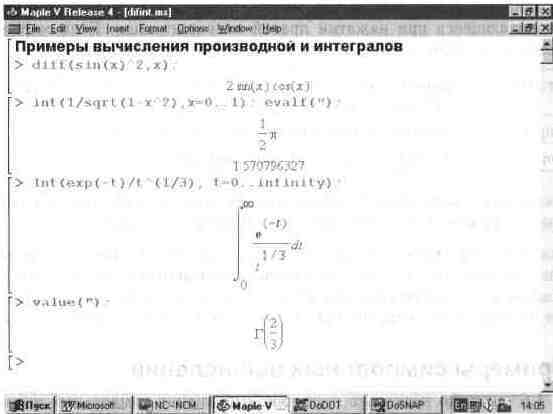
Рис. 1.7. Примеры вычисления производной и неопределенных интегралов

Примеры символьных вычислений

29

Обратите внимание на функцию Int — инертную форму функции int. Инертная форма служит для вывода записи интеграла в естественной математической форме, но с отложенным на потом выводом результата вычислении. Как отмечалось, это один из путей наглядной визуализации входных выражений. Все инертные функции имеют имя, начинающееся с прописной буквы, тогда как обычные функции имеют имена, начинающиеся с строчной буквы.

На рис. 1.8 показано вычисление интеграла,-имеющего закрытую форму. Как известно, такие интегралы не имеют представления через элементарные функции, но могут системой Maple V R4 вычисляться в численном виде.

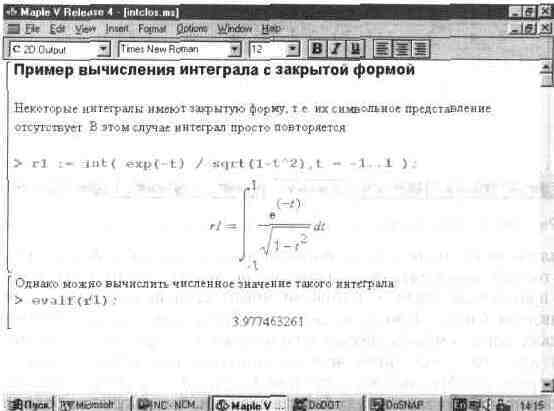
Рис. 1.8. Вычисление интеграла, имеющего закрытую форму.

Одной из проблем систем компьютерной алгебры является проблема разбухания результатов — как оконечных, так и промежуточных. Связано это с тем, что аналитическое представление порою даже для простых задач может оказаться весьма громоздким — пожалуй, это главная причина прохладного отношения к аналитическим вычислением со стороны инженеров, особенно практиков. К примеру, численное решение кубического уравнения не вызовет трудностей даже на калькуляторе [I], тогда как системы символьной математики выдают его в виде формул, едва умещающихся на экране дисплея. Это и иллюстрирует рис. 1.9, на котором показано решение квадратного уравнения (его знает каждый мало-мальски успевающий школьник) и решение кубического уравнения (оно вызывает бурный восторг или легкий шок — в зависимости от отношения учащегося к математике).

Обратите внимание на применение в записи результата специальной переменной % 1 для сокращения записи решения кубического уравнения. Переменные такого вида (%2, %3 и т.д.) могут встречаться в результатах решения и других задач. Могут также встречаться и другие обозначения — они будут описаны по мере появления в соответствующих примерах.

30

Установка системы и начало работы с ней

Рис. 1.9. Решение квадратного и кубического уравнения в символьной формг

Щепетильность системы в ее стремлении выдать полный и математически предельно точный результат, безусловно, очень важна для математиков. Но для многих прикладных задач, с которыми имеют дело инженеры и техники, она оборачивается боком. Инженеры часто прекрасно знают, какие из членов математических формул можно преспокойно отбросить, тогда как для математика-теоретика или аналитика такое действо типичное кощунство. Порою системы компьютерной алгебры выдают настолько «заумный» и огромный результат, что его упрощение может занять куда больше времени, чем получение более простого результата с заранее выполненными упрощениями. Впрочем, каждому свое! И Maple V имеет множество функций, обеспечивающих преобразование результатов в ту или иную форму.

Приведем еще один характерный пример — решение системы линейных уравнений с помощью функции solve (рис. 1.10). Обратите внимание на форму задания системы и выдачи результатов и поразительную естественность решения задачи.

Слова solve, diff и int с их аргументами являются именами встроенных в систему функций, возвращающих символьные значения результата. Обычному пользователю может стать дурно, когда он узнает, что таких функций с их вариантами в системе Maple V R4 почти 2500! Да к тому же многие функции (та же solve для решения уравнений) подчас могут применяться во многих случаях и имеют массу опций и директив для уточнения направлений решения и расширения областей применения.

В утешение можно отметить три важных обстоятельства: мало кто на практике из всей этой массы функций использует их более нескольких десятков, названия и формы представления многих функций интуитивно предсказуемы, система имеет превосходную справочную систему, с помощью которой при определенном терпении (и непременном желании) можно разобраться с любой из функций.

Работа с кнопками быстрого управления

31

Необходимые функции и правила их преобразования система черпает в библиотечном модуле размером более 12 Мбайт (он содержит файлы maple, hdb, maple.lib и maple.ind). Это иногда занимает время — особенно при первом использовании определенной группы операторов (например, тригонометрических). При повторном использовании этой группы система «обучается» (точнее, использует уже загруженные средства) и выполняет расчеты заметно быстрее.

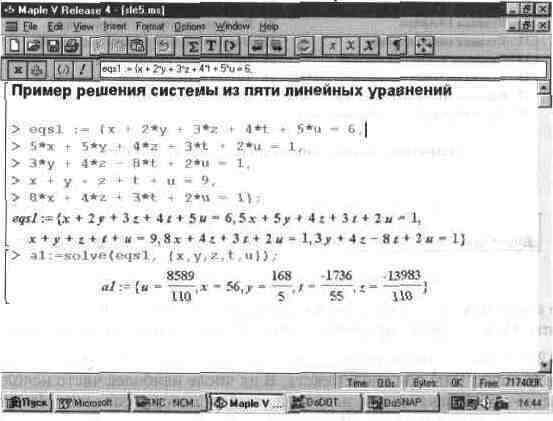
Рис. 1.10. Решение системы из четырех линейных уравнений.

1.5. Работа с кнопками быстрого управления

1.5.1. Работа с панелью инструментов

Пока мы в проведении вычислений пользовались лишь простейшими средствами управления системой — вводом выражений и текстовых надписей с клавишного пульта. Теперь пора расширить представления о работе с системой. Прежде чем работать с главным меню, надо отметить, что для многих (особенно начинающих) пользователей удобно работать с кнопками быстрого управления системой, расположенными на панелях управления и форматирования, которые находятся прямо под строкой главного меню.

На рис. 1.11 показано назначение кнопок панели управления (Tool Bar). Эти кнопки дублируют наиболее важные операции главного меню и имеют наглядные и типовые для Windows-приложений обозначения.

При необходимости панель инструментов можно убрать (см. главу 4). Окна графики также имеют свои панели инструментов. Их описание дано в главе 7.

1.5.2. Работа с панелями форматирования

Другое полезное средство для облегчения работы по форматированию текстов, входных математических выражений и графиков — панели форматирования.

32

Установка системы и начало работы с ней

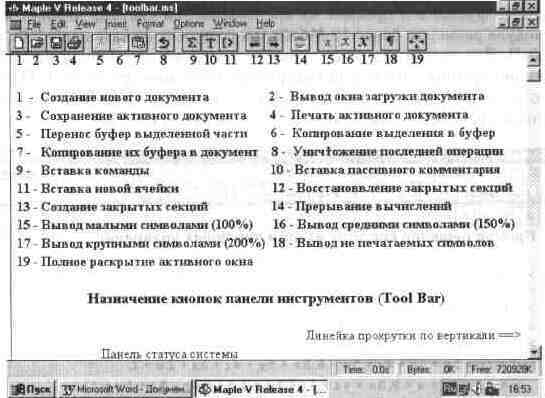
Рис. 1.11. Назначение кнопок панели управления.

Обычно выводится одна панель форматирования, соответствующая текущему режиму работы. Панели форматирования Context Bar являются контекстно-зависимыми.

Рис. 1.12 показывает назначение средств, которые находятся на панели форматирования (Context Bar) при вводе текста. В их числе наиболее часто используемые средства — установка стиля надписей, выбор набора символов (шрифтов) и установка размера символов. Часто используются также кнопки для задания полужирных (Bold), курсивных (Italic) и подчеркнутых (Underline) символов.

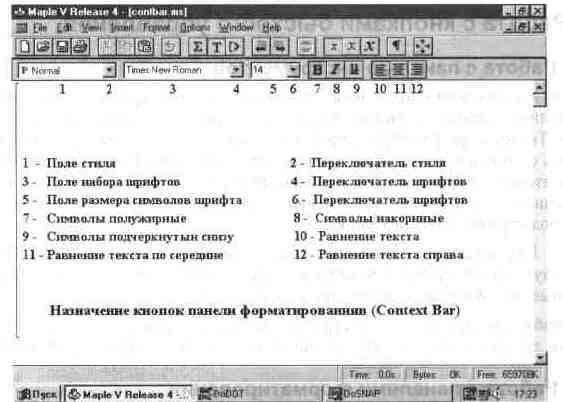
Рис. 1.12. Назначение средств управления панели форматирования текста.

Работа с системой помощи 33

Полезно при работе с системой следить и за информацией в панели статуса системы (внизу экрана). В ней появляются надписи, поясняющие исполняемые операции. Кроме того, выводится текущее время, объем используемой памяти и объем памяти раздела диска, на котором установлена система. Как отмечалось (рис. 1.5), при наборе входных выражений панель форматирования приобретает иной вид.

Панель статуса имеет вид линии (Status Line)' внизу документа и отображает различную полезную и оперативную информацию — прежде всего о текущем времени и использовании памяти. Она также выдает контекстно-зависимые сообщения о характере работы с системой.

Хотя панели управления, форматирования и статуса удобны для быстрого управления системой, они обладают одним существенным недостатком — занимают часть площади экрана. Однако в позиции View главного меню имеются опции, позволяющие убрать с экрана любую из этих панелей или все их. В приведенных выше примерах применения системы Maple V R4 использовался этот прием.

1.6. Работа с системой помощи

Maple V R4 имеет две взаимосвязанные системы помощи. Одна из них онлайновая (online) позволяет вызвать нужную справку в командном режиме. Для этого достаточно набрать в командной строке слово help или ? (вопросительный знак) с последующим указанием искомого слова, например:

> help sin

или

>?sin

В данном случае после нажатия клавиши Enter будет получена справка по функции sin (рис. 1.13). Такое обращение применяется для библиотечных функций и зарезервированных (ключевых) слов системы. Его недостатком является то, что нужно знать имя оператора или функции, по которой ожидается получение справки.

При этом на экран дисплея будет выведено подробное сообщение (справка) на английском языке о назначении и правилах записи (синтаксисе) соответствующей функции, оператора или пакета применений. Весьма полезным средством является выделение и выбор примеров из справок. Для этого используется клавиша Ins, которой намечают начало и конец выделений. Можно также выделить пример, перемещая мышь с нажатой левой клавишей. Наконец, используя команду Сору Examples в позиции Edit главного меню окна справки (рис. 1.13), можно скопировать в буфер все примеры.

После этого, закрыв окно справки, можно с помощью команды Paste в позиции Edit главного меню документа перенести в него имеющиеся в буфере примеры. Это показано на рис. 1.14.

Таким образом, можно легко проверить работу примеров по любой функции системы. Как правило, дается несколько примеров на применение каждой функции, так что общее число примеров трудно представить, поскольку число функций достигает двух тысяч.

Помимо встроенных в ядро функций в систему входят дополнительные функции и пакеты прикладных программ. Чтобы получить помощь по ним, нужно ввести

34

Установка системы и начало работы с ней

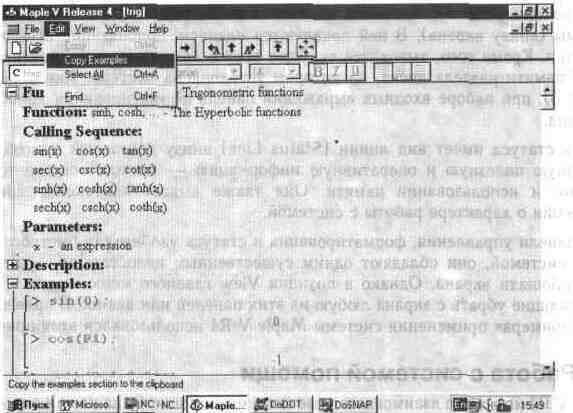
Рис. 1.13. Пример получения справки по функции sin.

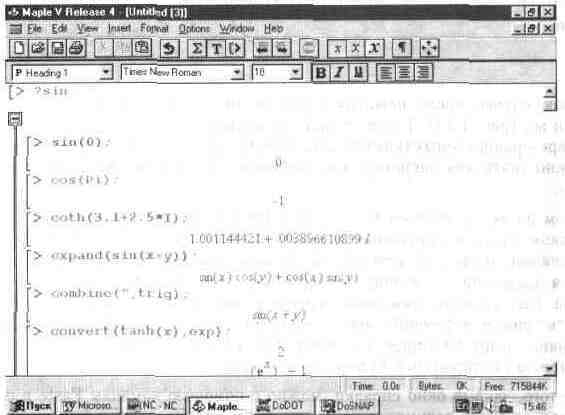
Рис. 1.14. Примеры, скопированные в документ.

их имя после вопросительного знака. Например, чтобы получить помощь по функциям пакета расширения системы plots, достаточно ввести в командной строке:

> ?plots А чтобы найти полный перечень пакетов расширения, можно ввести команду:

> ?packages

Главное меню системы и «горячие» клавиши

35

Обратите внимание на то, что после этих обращении к справочной системе никакие знаки (двоеточие или точка с запятой) не ставятся. В конце каждой справки приводятся имена связанных с данным объектом слов, а также другие возможные формы получения справок. Используя их, можно более подробно познакомиться с возможностями системы.

Удобно в описываемой версии Maple V решен и вопрос о предоставлении оперативной контекстно-зависимой справки по любой функции. Достаточно указать ее маркером и нажать клавиши Ctrl + F1 (или, что не документировано, просто F1). Тут же будет выведено окно справки по данной функции. Можно также выделить интересующее вас слово и получить справку по нему.

1.7. Главное меню системы и «горячие» клавиши

Главное меню системы Maple V R4 расположено непосредственно под титульной строкой. Оно дает доступ к основным операциям и опциям, присущим пользовательскому интерфейсу системы. Ниже дан перечень позиций (подменю) главного меню в режиме открытого документа:

File	Работа с файлами и печатающим устройством.
Edit	Редактирование документа и операции с буфером.
View	Управление видом пользовательского интерфейса.
Insert	Операции вставки.
Format	Операции задания форматов.
Options	Задание опций.
Window	Управление окнами.
Help	Работа со справочной системой.

Если все документы закрыты, то главное меню имеет только две позиции — File и Help. При этом место для окон документов пусто и окрашено в серый цвет (рис. 1.15). Позиция File имеет подменю всего с тремя операциями — это подменю также показано на рис. 1.15.

Для активизации позиций главного меню можно использовать сочетание клавиши Alt с одной из клавиш, выделенной в названии требуемой позиции подчеркиванием снизу. Такое сочетание клавиш получило название «горячих» клавиш (Hot Keys) управления.

Активизация позиций главного меню
Открытие подменю Edit	Alt + Е
Открытие подменю File	Alt + F
Открытие подменю Format	Alt + R
Открытие подменю помощи Help	Alt + H
Открытие подменю вставок Insert	Alt + I
Открытие подменю опций Options	Alt + 0
Открытие подменю вида View	Alt + V
Открытие подменю управления окнами Window	Alt + W

36

Установка системы и начало работы с ней

Рис. 1.15. Вид экрана Maple V R4 при всех закрытых документах.

Возможна активизация позиции главного меню и прямым указанием на них курсором мыши с быстрым нажатием ее левой клавиши. «Горячие» клавиши присвоены и многим другим наиболее распространенным операциям, которые облегчают и ускоряют (наряду с кнопками панелей управления и форматирования) быстрое управление системой. Ниже приведен список других «горячих» клавиш, разбитых на ряд категорий.
Задание стиля символов и режимы ввода текстов
Задание полужирных символов	Ctrl + В
Установка курсивных символов	Ctrl + I
Задание подчеркивания символов Underline	Ctrl + U
Включение/выключение ввода текста	F5
Установка режим ввода (Input Mode)	Ctrl + M
Задание режима ввода текста Text Input Mode	Ctrl + Т
Операции выделения
Плавное выделение от маркера влево	Shift	+ <-
Плавное выделение от маркера вправо	Shift	+-,
Плавное выделение от маркера вверх	Shift	+r
Плавное выделение от маркера вниз	Shift	+.1
Выделение от маркера до начала строки	Shift	+ Home
Выделение от маркера до конца строки	Shift	+ End
Выделение от курсора влево и до начала документа	Shift	+ Pg Up
Выделение от курсора вправо и до конца документа	Shift	+ PgDn

Главное меню системы и «горячие» клавиши

37

Операции удаления, вставки и замены
Копирование выделенных объектов в буфер	Ctrl + С
Перенос выделенных объектов из документа в буфер	Ctrl + X
Вставка данных из буфера Paste	Ctrl + V
Удаление указанного объекта	Ctrl + Delete
Закрытие выделенной секции	Ctrl + .
Поиск вхождений	Ctrl + F
Вставка исполняемой группы ...После маркера	Ctrl + J
...До маркера	Ctrl + К
Вставка параграфа ...До маркера	Shift + Ctrl + J
...После маркера	Shift + Ctrl + К
Восстановление закрытых секций (Outdent)	Ctrl + ,
Переходы по документу
Переход к началу линии	Home
Переход в конец документа	Ctrl + End
Переход к концу линии	End
Переход в начало документа	Ctrl + Home
Создание новой строки	Shift + Enter
Перемещение к следующей линии ввода	Tab
Перемещение к предыдущей линии ввода	Shift + Tab
Создание, загрузка, сохранение и печать документа
Создание нового документа	Ctrl + N
Вызов окна загрузки документов Open	Ctrl + 0
Запись документа с текущим именем Save Worksheet	Ctrl + S
Запись документа с текущим именем Save Worksheet	Ctrl + S
Печать документов Print Worksheet	Ctrl + P
Закрытие активного окна (документа)	Ctrl + F4
Завершение работы с Maple (Exit)	Alt + F4
Операции просмотра
Восстановление экрана Redraw Screen	Ctrl + L
Просмотр Show Region Ranges	F9
Просмотр Show Section Ranges	Shift + F9
Разделение строки на две части Split Group	F3
Объединение смежных строк Join Group	F4
Разделение секций на две части Split Section Shift	F3
Объединение смежных секций Join Section Shift	F4

38

Установка системы и начало работы с ней

Отмена предшестиующей операции Undo Delete	Ctrl + Z
Установка размеров символов
Размер (Zoom Factor) 50%	Ctrl + 1
Размер 100%	Ctrl + 2
Размер 150%	Ctrl + 3
Размер 200%	Ctrl + 4
Размер 300%	Ctrl + 5
Размер 400%	Ctrl + 6

Разумеется, можно успешно работать с системой, вообще ничего не зная про «горячие» клавиши. Однако быстрое и профессиональное пользование системой Maple V R4 предполагает пользование этими клавишами, поскольку при этом реализуется минимум операций, нужных для ввода той или иной функции управления системой.

При работе с русифицированной версией Windows 95 нередко латинские буквы в обозначениях «горячих» клавиш заменяются русскими буквами, не несущими никакого смыслового значения о выполняемой операции. В этом случае полезно знать, что соответствующая латинская буква (или иной знак) находятся на той клавише, которая имеет русскую букву.

1.8. Особенности версии Maple V R3

Третья реализация системы Maple V вполне современная математическая система, которая по своим математическим возможностям практически почти не уступает новым реализациям R4 и R5. Ее главное отличие от этих реализации — несколько упрощенный пользовательский интерфейс. Это видно из рис. 1.16.

Рис. 1.16. Экран математической системы Maple V R3.

Особенности версии Maple V R3

39

На экране можно обнаружить уже описанные кнопки быстрого управления, хотя и в меньшем количестве, чем у реализации R4. Надо отметить, что тенденция к увеличению числа таких кнопок проявляется все реже, поскольку разобраться в их назначении оказалось не проще, чем в многочисленных пунктах главного меню. Поэтому система Maple V R3 по-прежнему пользуется успехом.

Еще одна отличительная деталь этой реализации системы — заимствованная из версий под MS-DOS организация справочной системы виде последовательного поиска нужной функции. Этот поиск напоминает работу с тематическим каталогом и сводится к постепенному уточнению назначения искомой функции (рис. 1.17).

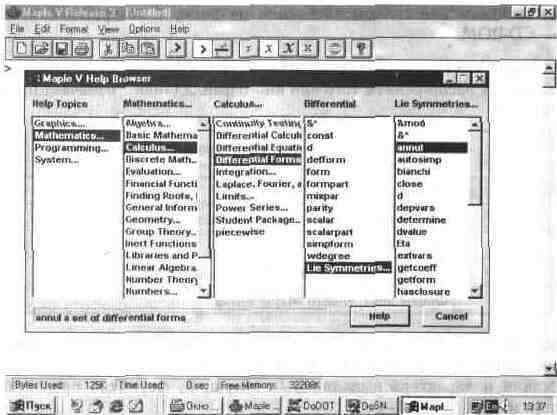
Рис. 1.17. Поиск нужной функции в базе данных справочной системы Maple V R3.

В реализации R4 создатели Maple V отказались от этой довольно удачной находки, сделав справочную систему подобной справочным системам большинства приложений под Windows, например, таких, как компоненты системы Microsoft Office. Тем самым они выплеснули ребенка вместе с водой.

Тем временем разработчики конкурирующей системы Mathematica 3, напротив, ввели подобную справочную систему в свой продукт. Спохватившись, Maple Software восстановила статус-кво своей справочной системы Maple V, включив тематический поиск в указанном виде в свою новейшую реализацию Maple V R5. Надо отметить, что только благодаря удачной справочной системе многие пользователи реализацией R3 предпочитают ее более новым реализациям R4 и R5. Особенностям последней посвящена глава 14.