Глава 12. Пакеты расширений Maple V и работа с ними

12.1. Назначение пакетов расширения и обращение к ним

Как уже отмечалось, некоторые функции системы Maple помимо ядра могут находится в стандартной библиотеке и в пакетах расширения, входящих в базовую поставку системы. Это значит, что их не надо приобретать дополнительно. Однако перед использованием таких функции их надо загрузить или отдельно или целым пакетом, если большинство его функций представляет интерес для пользователя.

В этой главе дается выборочная информация о функциях, содержащихся в пакетах расширения. Напоминаем, их список можно получить, используя команду

> ?packages

С помощью команды

> ?name_package

можно получить информацию о любом пакете расширения и найти список входящих в него функций. Названия пакетов и перечни их функций представлены в следующих разделах данной главы в начале каждого раздела. Поэтому распечатка имен пакетов и их назначений здесь не приводится.

Для обращения к функциям того или иного пакета используется его полная загрузка командой

> with(package)

Если вам необходима какая-то одна функция пакета или небольшая часть входящих в пакет функций, то не стоит загружать его целиком. Это может привести к избыточным затратам памяти компьютера и даже нарушить нормальную работу некоторых функций. Следует помнить, что нередко пакеты переопределяют некоторые функции ядра. Для загрузки избранных функций используется команда with в форме:

> with(package, f1, f2,...)

или

> with(package, [f1,f2,...])

При этом загружаются функции fl,f2,... из пакета с именем packages.

Может показаться, что было бы лучше иметь все функции в одном ядре. Однако создание ядра, реализующего все функции системы (в версии R4 их более 2500), неразумно. Во-первых, такое ядро будет занимать много места в памяти. А это усиливает его моральное старение. Во-вторых, это вызвало бы чрезмерные затраты памяти на хранение всех функций ядра, поскольку оно постоянно загружено в память компьютера.

Пакет решения дифференциальных уравнений DEtools 235

Поэтому в Maple V ядро содержит определенный (и довольно обширный) минимум хорошо апробированных функций, а большинство других функций размещается в стандартной библиотеке и в пакетах расширения. Они готовятся на Maple-языке программирования и могут легко модернизироваться. К тому же пакеты расширения могут модифицироваться (что не очень желательно) или дополняться (что приветствуется) пользователями. Некоторой платой за это является необходимость вызова того или иного пакета или функции перед их применением.

В этом разделе описана структура пакетов расширений системы Maple V R4. Объем книги не позволяет остановиться даже на описании синтаксических правил применения всех функций этих пакетов. Этого, кстати, нет и в книгах [37,38], входящих в поставку системы. Очевидно, в этом нет и особого смысла — подавляющее большинство функций представляют малый интерес для конкретного пользователя. Те же, кто ими интересуются, могут легко восполнить пробелы в их описании с помощью справочной системы.

Однако в описании состава каждого пакета в данной главе упомянуты своими именами все без исключения функции. Это позволяет оценить полноту того или иного пакета и без труда вызвать справочные листы по любой функции. Описание функций пакетов расширения дано выборочно, при этом предпочтение отдавалось тем функциям, которые используются в массовых математических и научно-технических расчетах.

Полезно отметить, что большинство функций имеет вполне понятные имена, отражающие их суть и назначение. К примеру, назначение функций animate или даже textplot в пакете plots или Diff, Int и Limit в пакете student понятны, пожалуй, всем. Но и в гораздо более специализированных пакетах имена входящих в них функций в значительной мере знакомы специалистам, поскольку почти всегда ассоциируются с общепринятыми названиями тех или иных специализированных функций или с их комбинациями.

12.2. Инструментальный пакет решения

дифференциальных уравнений DEtools

Решение дифференциальных уравнений самых различных типов — одно из достоинств системы Maple V. Пакет DEtools предоставляет ряд полезных функций для решения дифференциальных уравнений и систем с такими уравнениями:

DEnormal DEplot DEplot3d Dchangevar PDEchangecoords PDEplot autonomous convertAlg convertsys dfieldplot indicialeq phaseportrait reduceOrder regulars? translate untranslate varparam

Этот пакет дает самые изысканные средства для аналитического и численного решения дифференциальных уравнений и систем с ними. Поскольку этих функций не очень много и они широко используются в практике математических расчетов, приведем их полные наименования:

DEnormal	Возвращает нормализованную форму дифференциальных уравнений.
DEplot	Строит графики решения дифференциальных уравнении.

236

Пакеты расширений Maple V и работа с ними

DEplot3d	Строит трехмерные графики для решения систем дифференциальных уравнении.
Dchangevar	Изменяет переменные в дифференциальных уравнениях.
PDEchangecoords	Изменяет координатные системы для дифференциальных уравнений в частных произвордных.
PDEplot	Строит графики решения дифференциальных уравнении в частных производных.
autonomous	Тестирует дифференциальные уравнения на автономность.
convertAlg	Возвращает лист коэффициентов для дифференциальных уравнении.
convertsys	Преобразует систему дифференциальных уравнении в систему одиночных уравнении.
dfieldplot	Строит график решения дифференциальных уравнении в виде векторного поля.
indicialeq	Преобразует дифференциальные уравнения в полиномиальные.
phaseportrait	Строит график решения дифференциальных уравнений в форме фазового портрета.
reduceOrder	Понижает порядок дифференциальных уравнении.
regulars?	Вычисляет регулярные особые точки для дифференциальных уравнении второго порядка.
translate	Преобразует дифференциальные уравнения в лист операторов.
untranslate	Преобразует лист операторов в дифференциальные уравнения.
varparam	Находит общее решение дифференциальных уравнении методом вариации параметров.

Функции построения графиков решения дифференциальных уравнении будут описаны в главе 13, целиком посвященной графическим возможностям Maple V R4. Здесь же мы рассмотрим другие функции пакета Detools. Для использования функций этого пакета он должен быть загружен командой:

> with(DEtools):

Функция

autonomous(des,vars,ivar)

тестирует дифференциальное уравнение (или систему) des. Ее параметрами, помимо des, являются независимая переменная ivar и зависимая переменная dvar. Следующие примеры поясняют применение этой функции:

>autonomous(sin(z(t)-z(t)д2)»(D@@4)(z)(t)-cos(z(t))-5,z,t);

true

> DE:=diff(x(s),s)-x(s)*cos(arctan(x(s)))=arctan(s):

> autonomous(DE,{x},s);

false

Функция Dchangevar используется для обеспечения замен (подстановок) в дифференциальных уравнениях:

Dchangevar(trans, deqns, c_ivar, n_ivar) Dchangevar(tranl, tran2, .... tranN, deqns, c_ivar, n_ivar)

Пакет решения дифференциальных уравнений DEtools 237

В первом случае trans — список или множество уравнений, которые подставляются в дифференциальное уравнение, список или множество дифференциальных уравнений deqns. При этом c_ivar — имя текущей переменной, n_ivar — имя новой переменной (задается опционально).

Во второй форме для подстановки используются уравнения trani, tran2, .... Ниже представлены примеры применения функции Dchangevar:

> with(DEtools):

Преобразование 1-го типа

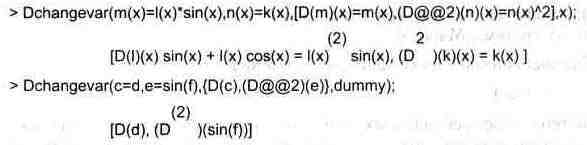
Пробразование 2-го типа

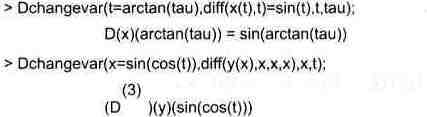
Преобразование 3-го типа

Дополнительные примеры

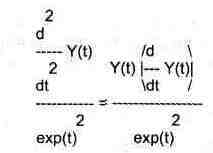
Следует отметить, что подстановки являются мощным средством решения дифференциальных уравнении. Нередки случаи, когда дифференциальное уравнение не решается без их применения.

Примеры использования подстановок можно найти в [35] и в примерах справочной базы данных системы Maple V.

Функция DEnormal синтаксически записывается в виде DEnormal(des,ivar,dvar),

где des — система дифференциальных уравнений, ivar — независимая переменная, dvar — зависимая переменная. Применение этой функции поясняют следующие примеры:

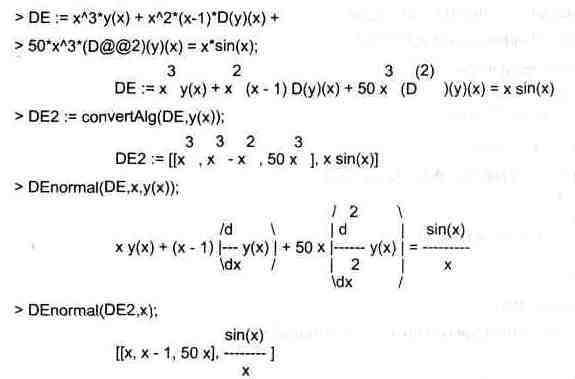
Функция convertAlg(des,dvar) возвращает лист коэффициентов формы системы дифференциальных уравнений des с зависимыми переменными dvar. Это поясняют следующие примеры:

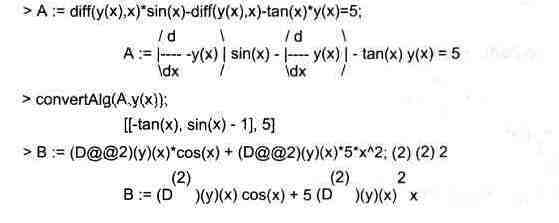
> convertAlg(B.y(x));

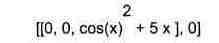
Для изменения переменных в системах дифференциальных уравнений используется функция:

convertsys(deqns, inits, vars, ivar, yvec, ypvec)

Здесь: deqns — одно дифференциальное уравнение или лист (множество), представляющие систему дифференциальных уравнении первого порядка, inits — множество или лист начальных условий, vars — зависимые переменные, ivar — независимые переменные, yvec — вектор решений, ypvec — вектор производных.

Функция indicialeq(des,ivar,alpha,dvar)

обеспечивает полиномиальное представление для линейного гомогенного дифференциального уравнения второго порядка des. Параметр alpha намечает точку сингулярности.

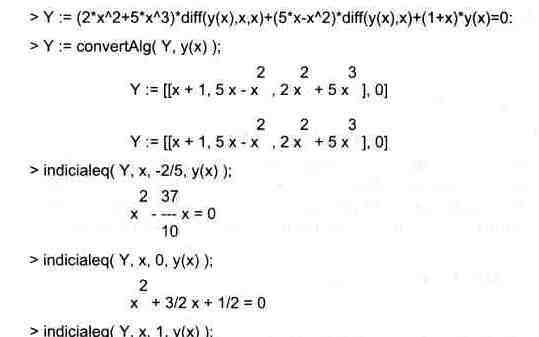
Error, (in DEtools/indicialeq/indicial) 1, is not a regular singular point. Функция

reduce0rder(des,dvar,partsol, solutionForm)

обеспечивает понижение порядка дифференциального уравнения des (или системы уравнений, представленных списком или множеством) при зависимых переменных dvar, частном решении partsol (или листе частных решений) и флаге solutionForm, показывающем, что решение происходит явным методом (explicitly).

Для демонстрации действия этой функции воспользуемся примером из справочной страницы по ней:

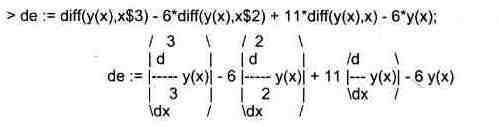
> sol := exp(x):

sol := exp(x)

> reduce0rder( de, y(x), sol);

/ 2 \

¦ d ¦ /d \

I-- y(x)¦ - 3 - y(x)¦ + 2 y(x)

¦ 2 ¦ \dx /

\dx /

> reduce0rder( de, y(x), sol, basis);

[exp(x), exp(2 x), 1/2 exp(3 x)]

Функция regularsp(des,ivar,dvar)

вычисляет регулярные особые (сингулярные) точки для дифференциального уравнения второго порядка или системы дифференциальных уравнений des.

Следующий пример поясняет применение данной функции:

> coefs := [21 '•{^2 - x + ^.О.ЮСГх^х--!)^]:

> regularsp(coefs, x);

[О, 1]

Еще две функции пакета Detools translate(des,ivar,pt,dvar) и untranslate(des,ivar,pt,dvar)

выполняют особую операцию трансляции дифференциального уравнения (или

списка дифференциальных уравнений) из центрированного относительно 0 в центрированный относительно 1 и наоборот. С деталями этого специфического процесса заинтересованный читатель может познакомиться в справочной базе

данных.

Наконец, еще одна полезная функция пакета varparam(sols,v,ivar)

находит общее решение дифференциального уравнения (или системы уравнений) sols методом вариации параметров. Параметр v задает правую часть уравнения, если он равен 0, ищется только частичное решение.

Приведенные ниже примеры показывают работу с этой функцией:

> de := diff(Y(x),x,x) + Y(x):

> sols := dsolve( de, Y(x), output=basis);

sols := (cos(x), sin(x)]

> varparam( sols, csch(x), x );

/ /

_C[1] cos(x) + _C[2] sin(x) + ¦ -sin(x) csch(x) dx cos(x) + ¦ cos(x) csch(x) dx\

I I / /

sin(x)

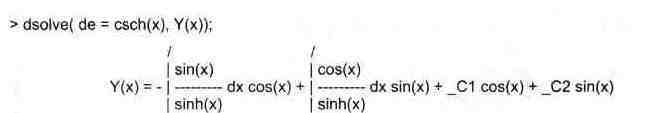
> varparam( [exp(3*x),exp(-x)], ехр(х), х );

_С[1] ехр(3 х) + _С[2] ехр(-х) - 1/8 ехр(-2 х) ехр(3 х) -1/8 ехр(2 х)ехр(-х)

Более подробную информацию об этих функциях читатель найдет в справочных страницах по ним, а также в информационном документе detools.mws, содержащем систематизированное описание пакета Setools с многочисленными примерами его применения.

12.3. Пакеты функций комбинаторики

12.3.1. Пакет combinat

Функции комбинаторики достаточно известны из обычного курса математики. В пакете combinat представлено 32 функции комбинаторики:

Chi	bell	binomial	cartprod	character
choose	composition	conjpart	decodepart	encodepart
[ibonacci	firstpart	graycode i	nttovec	lastpart
multinomial	nextpart	numbcomb	numbcomp	numbpart
numbperm	partition	permute	powerset	prevpart
randcomb	randpart	randperm	stirlingi	stirling2
subsets	vectoint

Назначение этих функции (за исключением специфической функции Чи — Chi) следующее:

bell(n)	Возвращает Белл-число ехр(ехр(х)-!) = sum(bell(n)/n!*x"n, n=0..infinity), причем для вычислений используется рекуррентное соотношение bell(n+l) = (bellO+D'n.
binomial(n, r)	Возвращает биноминальные коэффициенты, причем если п и r целые числа, удовлетворяющие условию 0 < r < п, то функция возвращает С(п,г)=п!/(г!(п-г)!), а в общем случае C(n,r)=((n+l)/(((n+l)(((n-r+l)).
composition^, k)	Возвращает списки композиции для целых неотрицательных пир.
fibonacci(n)	Возвращает числа Фибоначчи, вычисляемые по рекуррентной формуле F(n) = F(n-l) + F(n-2), где F(0) = 0 и F(1) = 1.
fibonacci(n, х)	Возвращает значение полинома Фибоначчи F(n, х) = х F(n-l, х) + F(n-2, х), где F(0, х) = 0 и F(1, х) = 1, при этом F(n) = F(n, 1).
[irstpart(n)	Возвращает первую часть канонической последовательности ряда.
nextpart(l)	Возвращает следующую часть канонической последовательности ряда.
lastpart(n)	Возвращает последнюю часть канонической последовательности ряда.
prevpart(l)	Возвращает предыдущую часть канонической последовательности ряда.

conjpart(l)	11 Возвращает объединенный раздел в канонической последовательности ряда.
graycode(n)	Возвращает лист кодов Грея для п-битовых чисел.
multinomiaKn, kl, k2, ..„ km)	Возвращает мультиномиальные коэффициенты.
numbcomb(n) и numbcomb(n, m)	Возвращает число комбинации.
numbcomp(n, k)	Возвращает число композиций.
numbpart(n)	Возвращает список всех возможных сумм, дающих n.
permute(n) и permute(n, r)	Возвращает numbperm(n, r) = nops(permute(n, r)).
powerset(s)	Возвращает степень множества в множестве s.
randcomb(n, m)	Возвращает случайную комбинацию.
randpart(n)	Возвращает случайную часть.
randperm(n)	Возвращает случайную композицию.
stirlingl(n, m)	Возвращает число Стирлинга первого рода.
stirling2(n, m)	Возвращает число Стирлинга второго рода.
subsets(L)	Задает итерационную процедуру над степенями множества или листа L.
vectoint(l)	Возвращает индекс вектора канонического упорядочения 1.
inttovec(m. n)	Возвращает вектор канонического упорядочения для неотрицательных целых чисел тип.

Ниже даны примеры применения некоторых из этих функции:

> with(combinat):

> choose(4,3);

{{1,2,3}, {1,2, 4}, {1,3, 4}, {2, 3,4}} > choose([a, b, b]);

[[],[b],[b,b],[a],[a,b],[a,b,b]] > choose({a, b, c});

{{}, {a, b}, {a, b, c}, {b, c}, {c}, {a, c}, {a}, {b}} > choose([a, a, b, c], 3);

[[a, a, b], [a, a, c], [a, b, c]]

> composition(3,2);

{[2,1], [1,2]} > partition(4);

[[1.1, 1,1], [1,1,2], [2,2], [1,3], [4]] > decodepart(4,2);

[1,1,2] > fibonacci(6);

8 > seq(fibonacci(i),i=1..12);

1, 1,2,3,5,8, 13,21,34,55,89, 144

> partition(b);

[[1, 1, 1. 1, 1], [1, 1, 1, 2], [1,2, 2], [1. 1,3], [2, 3], [1,4], [5]] > firstpart(3);

[1,1,1] > nextpart(");

[1,2] > nextpart(");

[3] > prevpart(");

[1,2] > lastpart(3);

[3] > conjpart(");

[1,1,1] > conjpart(");

[3] g := graycode(3);

> printf(cat(' %.3d'$8), op(map(convert, g, binary))); lprint();

g :=[0, 1,3,2,6,7,5,4]

000001 011 010 110 111 101 100

> multinomial(8, 2, 6);

28 > multinomial(8, 2, 3, 3);

560 > numbcomp(8, 5);

35 > numbpart(3);

3

> partition(3);

[[1,1.1],[1,2},[3]] [[1, 1, 1, 1, 1], [1, 1. 1,2], [1, 2, 2], [1, 1, 3], [2, 3], [1,4], [5]]

> numbperm(4);

24 > numbperm(4, 3);

24 > numbperm([a, b]);

2 > numbperm({a, b, с}, 2);

6 > numbperm([a, a, b], 2);

3

> partition(J);

[[1,1,1],[1,2],[3]]

>permute(3, 2);

[[1,2], [1,3], [2,1], [2,3], [3,1], [3,2]]

> permute([a, a, b], 2);

[[а, а], [а, b], [Ь, а]] > powerset([a,b,b]);

[[].[b],[b,b],[a],[a.b],[a,b,b]] > randcomb([a, b, с, d]. 3);

[b, с, d] > randcomb([a, b, с, d], 3);

[a, b, d] > randcomb([a, b, c, d], 3);

[a, c, d] >randpart(10);

[1,1,8] > randpart(10);

[3,7] >stirling1(10,5);

-269325 >stirling2(10,5);

42525 > S := subsets({1, 2}):

> while not S[finished] do S[nextvalue]() od;

{} {1} {2} {1,2}

>vectoint([1,0,0]);

1 > inttovec(6,3);

[1,0,1]

12.3.2. Пакет combstruct

Еще 9 функций, относящихся к структурам комбинаторики содержит пакет combstruct:

allstructs count draw finished iterstructs nextstruct options specification .structures

Эти функции служат для создания случайно однородных объектов, принадлежащих заданному комбинаторному классу. Они становятся доступными при исполнении команды

> with(combstruct);

Например:

> allstructs(Subset({one,two}));

{{}, {two, one}, {one}, {two}}

>allstructs(Permutation([x,y,z]),size=2);

[[x. y], [x, z], [y, x], [y, z], [z, x], [z, y]]

>count(Subset({1,2,3}));

8 > draw(Combination(5),size=4);

{1,3,4,5} > count(Permutation([a,a,b]));

3 > it :=iterstructs(Permutation([a,a,b]),size=2):

> draw(Partition(9));

[2, 2, 5] > allstructs(Composition(3), size=2);

[[2,1], [1.2]]

Для более полного знакомства с этими специфическими функциями обратитесь к справочной системе.

12.4. Пакет финансово-экономических функций finance

Этот пакет представлен рядом функции в двух формах:

function(args) nnance[function](args)

Благодаря правилам задания аргументов можно реализовать практически все известные финансово-экономические расчеты, такие, как амортизация, накопления и платежи по вкладам и т.д. В свете задач рыночной экономики эти функции полезны для приверженцев решения всего не выходя из оболочки Maple. Все же надо отметить, что малозаметные тонкости в определении финансово-экономических функций затрудняют их применение. Есть множество специальных финансово-экономических пакетов, например, «Бухгалтерия 1С», которые лучше подходят для наших экономических реалий, чем «заумный» Maple V.

Для выполнения финансово-экономических расчетов используются две базовые конструкции функций:

function(args) и finance[function](args).

Полный перечень функций можно найти в справке по этому пакету. Ограничимся упоминанием нескольких наиболее характерных функций, связанных с использованием вкладов:

¦annuity(cash, rate, nperiods)

Вычисление суммы, находящейся на вкладе с начальным значением cash, процентом начисления rate и числом периодов nperiods.

cashflows(flows, rate)	Вычисление общей суммы вклада по списку вложении flows и проценту обесценивания денег rate.
futurevalue(amount, rate, nperiods)	Вычисление будущего значения вклада при начальном вложении amount, проценте начисления rate и числе периодов nperiods.
presentvalue(amount, rate, nperiods)	Вычисление начального вклада для получения суммы в amount при проценте начислении rate и числе вкладов nperiods.

Примеры применения этих функции даны ниже:

Поскольку формулы и обозначения в финансово-экономических расчетах в различной литературе (особенно в нашей и западной) несколько отличаются, это может создать серьезные ошибки при вычислениях. К примеру, в формулах Maple на самом деле используются не проценты начислений или обесценивания вкладов, а соответствующие им относительные единицы — например, 10% это есть 0,1. В нашей литературе проценты обычно задаются в явном виде, т.е. rate=10 при 10 процентах. Надо следить и за знаком величины rate, поскольку она может трактоваться как процент начислений или процент обесценивания денег по вкладам, в зависимости от того, какого она знака.

Расчеты подобного рода для Maple V относятся к самым простым, так что даже начинающий пользователь может составить свои функции для таких расчетов для вполне понятных ему и апробированных формул. Надо отметить однако, что используя символьное задание параметров формул легко получить вывод именно тех формул, которые использует система Maple, и сравнить их со своими формулами. В случае совпадения применение функций Maple возможно и предпочтительно.

12.5. Пакет геометрических расчетов geometry

Этот пакет содержит средства расчета основных параметров ряда геометрических объектов:

circle conic dsegment ellipse hyperbola

line parabola point segment square triangle

По каждому объекту возможно задание различных исходных параметров, так что пакет охватывает практически все виды классических геометрических расчетов. Несомненно, этот пакет заинтересует всех, кто работает в области геометрии и связанных с нею прикладных наук.

Обратите внимание на то, что функции этого пакета вовсе не строят графически соответствующие их названиям фигуры, а лишь выполняют типовые геометрические расчеты. Разумеется, в дальнейшем, используя данные этих расчетов, можно построить соответствующую фигуру с помощью функции графики.

Работу с пакетом поясним на примере одной из функций — circle. Она позволяет математически задать окружность и определить все ее геометрические параметры. Функция может иметь несколько форм записи. Например, в форме

circle(c, [А, В, С], n, 'centername'=m)

она определяет построение окружности, проходящей через три точки А, В и С. Необязательный параметр n — лист с именами координатных осей. Параметр 'centernarne'=m задает имя центра.

В форме

circle(c, [А, В], n, 'centername'=m )

задается окружность, проходящая через две точки А и В, а в форме

circle(c, [A, rad], n, 'centername'=m )

задается окружность, проходящая через одну точку А с заданным (и произвольным) радиусом rad и центром с.

Наконец, функция circle в форме circle(c, eqn, n, 'centername'=m )

позволяет задать окружность по заданному уравнению eqn и центру с. Проиллюстрируем применение функции circle на следующих примерах:

>detail(c1);

name of the object: c1

form of the object: circle2d

name of the center: 01

coordinates of the center: [1, 12/5]

radius of the circle: М2УЛ6'Э''(Л12)"1У[М'2.)

equation of the circle: m'^+n'^'m^^n = 0

Определим окружность с2, проходящую через две точки:

Аналогичным образом заинтересованный в таких расчетах читатель может ознакомиться с другими функциями самостоятельно. Тем более что в справочной системе на этот пакет имеется множество примеров работы с его функциями.

12.6. Пакет интегральных преобразований inttrans

Это один из наиболее важных для общематематических и научно-технических приложений пакетов. Он содержит небольшой набор функций:

addtable fourier fouriercos fouriersin hankel hilbert invfourier invhilbert invlaplace laplace melliri

Однако эти функции охватывают такие практические важные области математики, как ряды Фурье, прямые и обратные преобразования Лапласа и Фурье,

Z-преобразование и ряд других интегральных преобразований. Ниже они обсуждены более подробно.

12.6.1. Прямое и обратное преобразование Лапласа

Прямое преобразование Лапласа заключается в переводе некоторой функции времени f(t) в операторную форму F(p). Это преобразование означает вычисление интеграла

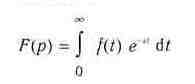
Для осуществления прямого преобразования Лапласа Maple V имеет функцию:

laplace(expr,t,p)

Здесь: ехрг — преобразуемое выражение, t — переменная, относительно которой записано ехрг, р — переменная, относительно которой записывается результат преобразования.

Обратное преобразование Лапласа означает переход от функции F(p) к функции f(t) с помощью формулы

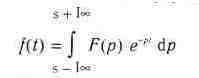
Для вычисления этого интеграла служит функция:

invlaplace(expr, р, t)

где: ехрг — выражение относительно переменной р, t — переменная, относительно которой записывается результирующая зависимость. Эта функция также размещается в пакете расширений inttrans.

Оба преобразования широко применяются в практике научно-технических вычислений и отражают суть операторного метода. При этом прямое преобразование создает изображение, а обратное — оригинал функции.

Ниже приведены примеры применения прямого и обратного преобразований Лапласа:

Нетрудно заметить, что в данном случае последовательное применение прямого, а затем обратного преобразования восстанавливает исходную функцию 4in(t)+a*cos(t).

12.6.2. Прямое и обратное преобразование Фурье

Прямое преобразование Фурье преобразует временную функцию f(t) из временной области в частотную и заключается в вычислении следующей интегральной функции:

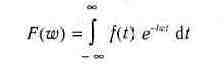
Оно реализуется следующей функцией пакета интегральных преобразований inttrans:

fourier(expr,t,w)

Здесь: expr — выражение (уравнение или множество), t — переменная, от которой зависит expr, w — переменная, относительно которой записывается результирующая функция.

Обратное преобразование Фурье задается вычислением интеграла:

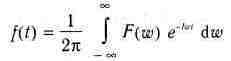
Оно фактически переводит представление сигнала в частотной области во временное представление.

Примеры преобразования Фурье представлены ниже:

Обратите внимание на то, что даже в простом первом примере применение обратного преобразования Фурье вслед за прямым не привело к буквальному восстановлению исходной функции sin(t) — потребовалась команда simplify, чтобы перевести результат в виде представления синуса через экспоненциальные функции к обычному виду sin(t).

12.6.3. Вычисление косинусного и синусного интегралов Фурье

Разложение функции f(t) в ряд Фурье требует вычисления интегралов следующего вида:

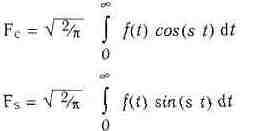
Они получили название косинусного и синусного интегралов Фурье и фактически задают вычисление коэффициентов ряда Фурье, в который может быть разложена функция f(t).

Для вычисления этих интегралов в пакете используются функции:

fouriercos(expr,t,s) и fouriersin(expr,t,s)

Поскольку формат задания этих функции вполне очевиден, ограничимся примерами их применения:

12.6.4. Интегральное преобразование Ханкеля

Интегральное преобразование Ханкеля задается следующим выражением:

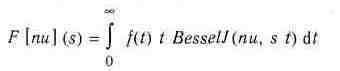
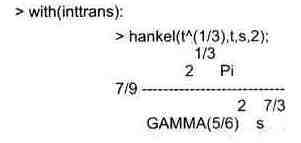
и выполняется функцией hankel(expr, t, s, nu)

Здесь: expr — выражение, равенство (или множство, или лист с выражениями/равенствами), t — переменная в expr, преобразуемая в параметр преобразования s, nu — порядок преобразования.

Следующий пример демонстрирует применение функции Ханкеля:

12.6.5. Прямое и обратное преобразования Гильберта

Прямое преобразование Гильберта задается следующим выражением:

и превращает функцию f(t) в F(s). Обратное преобразование Гильберта означает нахождение f(t) по заданной F(s). Эти преобразования выполняются функциями:

hilbert(expr, t, s), invhilbert(expr, t, s),

где назначения параметров очевидны. Приведенные ниже примеры иллюстрируют выполнение этих преобразований:

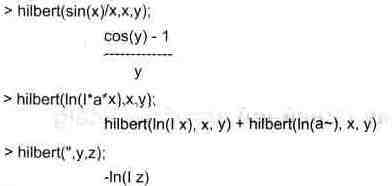
Как видно из этих примеров, обратное преобразование Гильберта, осуществленное над результатом прямого преобразования, не восстанавливает буквально функцию f(t).

12.6.6. Интегральное преобразование Меллина

Интегральное преобразование Меллина задается выражением

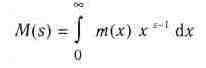
и реализуется функцией

mellin(expr, x, s)

с очевидными параметрами expr, x и s.

Применение преобразования Меллина иллюстрируют следующие примеры:

12.6.7. Функция addtable

Как видно из приведенных примеров, не всегда интегральные преобразования дают результат в явном виде. Получить его позволяет вспомогательная функция

addtable(tname,patt,expr,t,s)

где tname — наименование преобразования, для которого образец patt должен быть добавлен к таблице поиска. Остальные параметры очевидны.

Следующие примеры поясняют применение этой функции:

> with(inttrans):

> fouriersin(f(t),t,s);

fouriersin(f(t), t, s)

>addtable(fouriersin,f(t),F(s),t,s);

> fouriersin(f(x),x,z);

F(z)

12.7. Пакет решения задач линейной алгебры linalg 12.7.1. Состав пакета linalg

Это один из самых обширных и мощных пакетов в области решения задач линейной алгебры. Он содержит свыше ста функций, назначение которых указано ниже:

addcol	Формирует линейные комбинации из столбцов матрицы.
addrow	формирует линейные комбинации из строк матрицы.
adj	Возвращает матрицу, умножение которой на исходную квадратную матрицу дает единичную матрицу.
adjoint	Аналогична функции adj.
angle	Вычисляет угол между векторами.
augment	Объединяет две или больше матрицы горизонтально.
backsub	Обратная подстановка в матрице.
band	Создает ленточную матрицу.
basis	Находит базис для векторного пространства.
bezout	Создает Bezout-матрицу двух полиномов.
BlockDiagonal	Создает блок-диагональную матрицу.
blockmatrix	Создает блок-матрицу.
cholesky	Холески-декомпозиция квадратной положительно определенной матрицы.
charmat	Создает характеристическую матрицу.
charpoly	Возвращает характеристический полином матрицы.
col	Извлекает столбцы матрицы как векторы.
coldim	Определяет размерность столбца матрицы.
colspace	Вычисляет базис пространства столбца.
colspan	Вычисляет векторы охвата для места столбца.
companion	Вычисляет парную матрицу для полинома.
cond	Вычисляет условные числа матрицы. ;
copyinto	Перемещает элементы из одной матрицы в другую.
crossprod	Вычисляет векторное произведение.
curl	Вычисляет ротор вектора.
definite	Тест на положительные (отрицательные) определенные матрицы.
delcols	Удаляет столбцы матрицы.
delrows	Удаляет строки матрицы.
del	Вычисляет детерминант матрицы.
diag	Создает блок-диагональную матрицу.

Пакет решения задач линейной алгебры linalg

255

diverge	Вычисляет дивергенцию векторной функции.
dotprod	Вычисляет скалярное произведение векторов.
eigenvals	Вычисляет собственные значения матрицы.
eigenvects	Вычисляет собственные векторы матрицы.
entermatrix	Обеспечивает интерактивный ввод матрицы.
1 equal	Определяет, являются ли две матрицы равными.
exponential	Создает экспоненциальную матрицу.
extend	Расширяет матрицу.
ffgausselim	Свободное от дробей Гауссово устранение на матрице.
fibonacci	Матрица Фибоначчи.
forwardsub	Прямая подстановка в матрицу.
frobenius	Вычисляет форму Frobenius матрицы.
gausselim	Гауссово устранение на матрице. '
gaussjord	Синоним для rref (устранение Gauss-Jordan).
geneqns	Генерация элементов матрицы из уравнений.
genmatrix	Генерирует матрицу из коэффициентов уравнений.
grad	Градиент векторного выражения.
GramSchmidt	Вычисляет ортогональные векторы.
hadamard	Вычисляет ограничение на коэффициенты детерминанта.
hermite	Эрмитовая нормальная форма матрицы.
hessian	Вычисляет Hessian-матрицу выражения.
hilbert	Создает матрицу Гильберта.
htranspose	Находит Эрмитову транспонированную матрицу.
ihermite	Целочисленная Эрмитова нормальная форма.
indexfunc	Определяет функцию индексации массива.
innerprod	Вычисляет векторное произведение.
intbasis	Определить базис для пересечения пространства.
inverse	Вычисляет обратную матрицу.
ismith	Целочисленная нормальная форма Шмидта.
iszero	Проверяет, является ли матрица ноль-матрицей.
jacobian	Вычисляет якобиан матрицы векторной функции.
Jordan	Вычисляет форму матрицы Джордана.
JordanBlock	Возвращает блок-матрицу Джордана.
kernel	Вычисляет базис для нулевого промежутка.
laplacian	Вычисляет лапласиан.
leastsqrs	Решение уравнений по методу наименьших квадратов.
linsolve	Решение линейных уравнений.
Ludecomp	Существляет LU-декомпозицию.
matadd	Сложение матриц или векторов.

256

Пакеты расширений Maple V ч работа с ними

matrix	Создает матрицу.
minor	Вычисляет миноры матрицы.
minpoly	Вычисляет минимальный полином матрицы.
mulcol	Умножает столбец матрицы на заданное выражение.
mulrow	Умножает строку матрицы на заданное выражение.
multiply	Перемножение матриц или матрицы и вектора.
norm	Норма матрицы или вектора. .
normalize	Нормализация вектора.
orthog	Тест на ортогональность матрицы.
permanent	Вычисляет permanent матрицы.
pivot	Вращение относительно элементов матрицы.
potential	Вычисляет потенциал векторного поля.
Qrdecomp	Осуществляет QR-декомпозицию.
randmatrix	Генерирует случайные матрицы.
randvector	Генерирует случайные вектороы.
rank	Возвращает ранг матрицы.
ratform	Вычисляет рациональную каноническую форму (синоним для frobenius).
references	Выводит список основополагающих работ по линейной алгебре.
row	Извлекает строку матрицы как вектор.
rowdim	Определяет размерность строки матрицы.
rowspace	Вычисляет базис пространства строки.
rowspan	Вычисляет векторы охвата для места столбца.
rref	Сокращенная форма эшелона строки.
scalarmul	Умножение матрицы или вектора на заданное выражение.
singval	Вычисляет сингулярное значение матрицы.
singularvals	Вычисляет сингулярные значения матрицы.
smith	Вычисляет Шмидтову нормальную форму матрицы.
stack	Объединяет две или больше матрицы вертикально.
submatrix	Извлекает указанную субматрицу из матрицы.
subvector	Извлекает указанный вектор из матрицы.
sumbasis	Определяет базис для суммы векторных мест.
swapcol	Меняет два столбца в матрице.
swaprow	Меняет две строки в матрице.
Sylvester	Создает матрицу Сильвестра из двух полиномов.
toeplitz	Создает Toeplitz-матрицу.
trace	Возвращает след матрицы.
transpose	Вычисляет транспонированную матрицу.
vandermonde	Создает матрицу Вандервуда.
vecpotent	Вычисляет векторный потенциал.

vectdim : Определяет размерность вектора.
vector	Создает вектор.
wronskian	Матрица Вронскиана векторных функции.

Ниже мы рассмотрим более подробно только некоторые функции из этого пакета.

12.7.2. Интерактивный ввод матриц

Для интерактивного ввода матриц можно, определив размерность некоторого массива, использовать функцию entermatrix:

> with(linalg):

Warning, new definition for norm Warning, new definition for trace

>A:=array(1..3,1..3):

>entermatrix(A);

После исполнения этого фрагмента документа диалог с пользователем имеет следующий вид:

vector(n,list)	Задание вектора с п-элементами, заданными в списке.
matrix(n,m,list)	Задание матрицы с числом строк п и столбцов m с элементами. заданными списком list.

Ниже показано применение этих функции:

> V[2];

34

>М[1,3];

3

> М[2,3];

М[2, 3]

Обратите внимание на последние примеры, Они показывают задание вызова индексированных переменных вестора и матрицы.

12.7.4. Функции для работы с векторами и матрицами

Maple V имеет множество функций для работы с векторами и матрицами, входящими в библиотечный модуль linalg. Заметим, что с помощью команды ?name можно для любой функции получить справочную информацию с подробным ее описанием и примерами применения. Поэтому ограничимся приведением краткого описания наиболее распространенных функций для работы с векторами и матрицами.

Операции со структурой отдельного вектора V и матрицы М

coldim(M)	Возвращает число столбцов матрицы М.
rowdim(M)	Возвращает число строк матрицы М.
vectdim(V)	Возвращает число элементов вектора V.
col(M,i)	Возвращает i-й столбец матрицы М.
row(M.i)	Возвращает i-ю строку матрицы М.
minor(M,i,j)	Возвращает минор матрицы М для элемента с индексами i и J.
delcols(M,i.j)	Удаляет столбцы матрицы М от i-го до j-го.
delrows(V,i..j)	Удаляет строки матрицы М от i-й до j-й.
extend(M,m,n,x)	Расширяет матрицу М на m строк и п столбцов с применением заполнителя X.

Основные векторные и матричные операции

dotprod(U,V)	Возвращает скалярное произведение векторов U и V.
crossprod(U,V)	Возвращает векторное произведение векторов U и V.
norm(V) или norm(M)	Возвращает нормированный вектор или матрицу.
copyinto(A,B,i,j)	Копирует матрицу А в В для элементов последовательно от i до J.
concat(Ml,M2)	Возвращает объединенную матрицу с горизонтальным слиянием матриц Ml и М2
stack(Ml,M2)	Возвращает объединенную матрицу с вертикальным слиянием Ml и М2.
add(A.B) или evalm(A+B)	Возвращает сумму матриц А и В.
add(A,B,c,d)	Возвращает (с*А + d*B).
multiply(A,B) или evalm(A&*B)	Возвращает произведение матриц А и В.

Пакет решения задач линейной алгебры linalg

259

adjoint(M) или adj(M)	Возвращает сопряженную с М матрицу.
charpoly(M,lambda)	Возвращает характеристический полином матрицы М относительно заданной переменной lambda.
Eigenvals(M,vector)	Инертная форма функции, возвращающей собственные значения матрицы М и (при указании необязательного параметра vector) принадлежащие им вектора.
det(M)	Возвращает детерминант матрицы М.
jordan(M)	Возвращает матрицу М в форме Джордана.
hermite(M)	Возвращает матрицу М в Эрмитовой форме.
trace(M)	Возвращает след матрицы М.
rank(M)	Возвращает ранг матрицы М.
transpose(M)	Возвращает транспонированную матрицу М.
inverse(M) или evalm(l/M)	Возвращает обратную М матрицу.

Приведем примеры применения некоторых из этих фунщий:

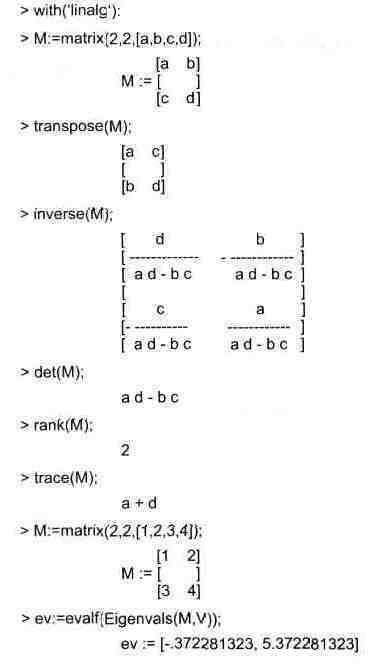
Читатель, понимающий суть матричных вычислении, легко справится с тестированием других функций, входящих в библиотечный модуль linalg.

В приведенных примерах полезно обратить внимание на то, что многие матричные функции способны выдавать результаты вычислений в аналитическом виде, что облегчает разбор выполняемых ими операций.

12.7.5. Решение систем линейных уравнений

Ниже представлен простой пример решения в символьном виде матричного уравнения с применением функций, входящих в модуль linalg:

Следующий пример показывает решение более сложной системы линейных уравнений с комплексными коэффициентами:

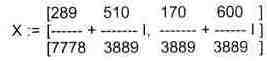
> Digits:=5: convert(eval(X),float);

[.037156 + .13114 I, .043713 + .15428 I]

На этот раз решение получено с использованием функции умножения матриц и вычисления обратной матрицы в виде X=A-1*B, т.е. в матричном виде. В конце примера показано преобразование результатов с целью их получения в обычной форме комплексных чисел с частями, представленными в форме чисел с плавающей точкой. Заметим, что аналогично решаются в численном виде системы линейных уравнений с действительными элементами матрицы А и вектора свободных членов В.

12.8. Пакет логических операций logic

Пакет logic содержит ряд функций, относящихся к математической логике:

bequal bsimp canon convert/MOD2 convert/Trominert convert/toinert distrib dual environ randbool satisfy tautology

Приведем определения этих функций:

bequal(bl,b2)	Возвращает логическое значение true, если логические выражения 111 и b2 эквивалентны, иначе возвращает false.
bequal(bl,b2,'p')	Проверяет логические выражения Ь1 и b2 на эквивалентность и задает результат логическим значением переменной р.
bsimp(b)	Упрощает логическое выражение b.
canon(b,alpha,form)	Представляет логическое выражение b в канонической форме.
convert(b,form,alphs)	Конвертирует b в заданную форму: /MOD2.
distrib(b,alpha)	Представляет b в виде суммы произведении.
dual(b)	Возвращает логическое выражение, дуальное b.
environ(n)	Задает уровень п (0,1,2,3) автоматического упрощения логических выражении.
randbool(alpha,b)	Создает случайное логическое выражение.
satisfy(b,alpha)	Подбирает переменные, соответствующие истинности b.
tautology(b,'p')	Тестирует b на тождественную истинность и помещает результат в р.

Ниже приведены примеры решения характерных задач математической логики:

>with(logic): bequal(x,x);

true > bequal(true,false);

false > bsimp(a &iff (a &or b)):

a &or (&not(b))

> convert(a &and b,MOD2);

ab > dual(a &or (&not a) = false);

a &and (&not(a)) = true > randbool({a,b});

(a &and b) &or ((&not(b)) &and (&not(a))) > randbool({a,b});

&or(a &and b, a &and (&not(b)), b &and (&not(a)))

> randbool({a,b});

a &and b > tautology(&and(a,b) &or (&not a) &or (&not b));

true > tautology((a &iff b) &or b,'p');

false

>P; .

{a = true, b = false}

Обратите внимание на применение функции randbool, поскольку она создает случайные логические выражения, то совпадения результатов ваших экспериментов с приведенными данными не будет.

12.9. Пакет функций теории графов networks

Графы широко используются при решении многих прикладных и фундаментальных задач. Пользователей, занятых решением таких задач, наверняка порадует пакет network, содержащий весьма представительный набор из 75 функций:

acycpoly	addedge	addvertex	adjacency	allpairs
ancestor	arrivals	bicomponents	charpoly	chrompoly
complement	complete	components	connect	connectivity
contract	countcuts	counttrees	cube	cycle
cyclebase	daughter	degreeseq	delete	departures
diameter	dinic	djspantree	dodecahedron	draw
duplicate	edges	ends	eweight	flow
flowpoly	fundcyc	getlabel	girth	graph
graphical	gsimp	gunion	head	icosahedron
incidence	incident	indegree	induce	isplanar
maxdegree	mincut	mindegree	neighbors	new
octahedron	outdegree	path	petersen	random
rank	rankpoly	shortpathtree	show	shrink
span	span poly	spantree	tail	tetrahedron
tuttepoly	vdegree	vertices	void	vweight

Теория графов используется достаточно широко даже при решении прикладных задач: например, вычисления оптимальных маршрутов движения железнодорож-

ных составов, наиболее целесообразной раскройки тканей и листов из различных материалов и т.д.

Рассмотрим некоторые избранные функции этого пакета, которые наиболее часто используются при работе с графами:

Функции создания графов

new	Создает пустой граф (без ребер и узлов).
void	Создает пустой граф (без ребер).
dublicate	Создает копию графа.
complete	Создает полный граф.
random	Возвращает случайный граф.
petersen	Создает граф Петерсена.

Функции модификации графов

addedges	Добавляет в граф ребро.
addvertecs	Добавляет в граф вершины.
connect	Соединяет одни заданные вершины с другими.
delete	Удаление из графа ребра или вершины.

Функции контроля структуры графов

draw	Рисует граф.
edges	Возвращает список ребер графа.
vertices	Возвращает список узлов графа.
show	Возвращает таблицу с полной информацией о графе.
ends	Возвращает имена вершин графа.
head	Возвращает имя вершины, которая является головой ребер.
tail	Возвращает имя вершины, которая является хвостом ребер.
incidence	Возвращает матрицу инцидентности.
adjacency	Возвращает матрицу смежности.
eweight	Возвращает веса ребер,
vweight	Возвращает веса вершин.
isplanar	Упрощает граф, удаляя циклы и повторяющиеся ребра, и проверяет его на планарность (возвращает true, если граф оказался планарным, и false — в противном случае).

функции с типовыми возможностями графов

flow	Находит максимальный поток в сети от одной заданной вершины к другой.
shortpathtree	Находит кратчайший путь в графе с помощью алгоритма Дейкстры.

Каждая из этих команд имеет одну или несколько синтаксических форм записи. Их можно уточнить при помощи справочной системы. С ее помощью можно ознакомиться и с назначением других функций этого обширного пакета. Проиллюстрируем его применение на нескольких типичных примерах.

На рис. 12.1 показан пример создания графа, имеющего четыре вершины, и графа Петерсона с выводом их графиков графической функцией draw.

Рис. 12.1. Построение графов (пример 1).

На рис. 12.2 показан другой пример работы с графами — построение графа функцией complete и затем его преобразование путем удаления части вершин. Исходный и преобразованный графы строятся функцией draw.

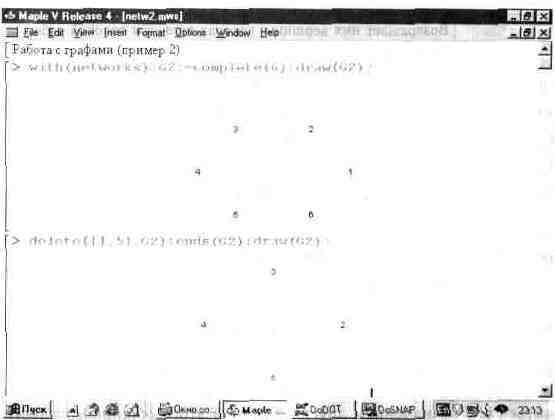
Рис. 12.2. Преобразование графа удалением части вершин (пример 2)

В третьем примере (рис. 12.3) граф формируется по частям. Вначале задается пустой граф функцией new, а затем с помощью функций addvertex и addedge в него включаются вершины и ребра. Далее функция connect соединяет вершину а с вершиной с, делая граф замкнутым. Функция draw строит сформированный таким образом граф, а функции head и tail используются для выявления голов и хвостов графа.

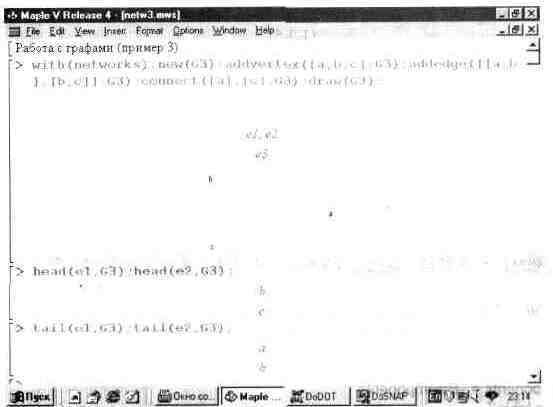
Рис. 12.3. Формирование графа и определение его голов и хвостов.

В четвертом примере, представленном на рис. 12.4, показано создание графа G2 (его рисунок дан на рис. 12.2) с вычислением для этого графа максимального потока от вершины 1. Обратите внимание, что в параметрах функции flow, использованной для этого, заданы две переменные: eset — принимает значение множества с ребрами, по которым проходит максимальный поток, и comp — принимает значение множества, в котором содержатся вершины, по которым проходит максимальный поток. Значения этих переменных выведены в области вывода. В конце этого примера дан пример применения функции shortpathtree, ищущей наиболее короткий путь от вершины 1 до других вершин.

Приведенный ниже пример иллюстрирует работу функции show, выдающую таблицу с полной информацией о графе, созданном функцией complete:

> with(networks):G2:=complete(4):

> show(G2);

table([

_Emaxname = 6

_Eweight = table([

e4= 1

e1 = 1

e6=1

e2=1

e5= 1

e3= 1

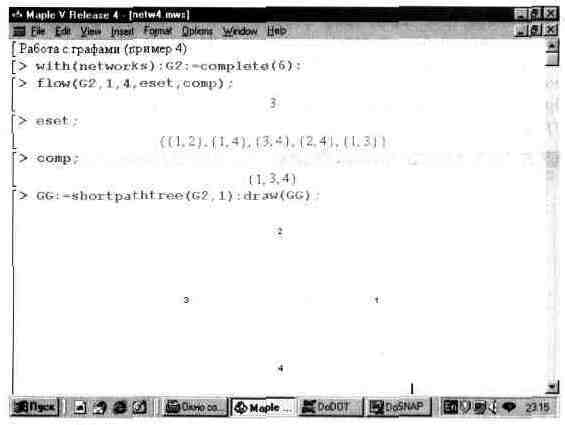
Рис. 12.4. Пример вычисления максимального потока и наиболее коротких путей для заданного графа.

])

_Bicomponents = _Bicomponents

_Ends = table([

e4 = {2, 3}

е1={1,2}

е6 = {1, 3}

е2={1,4}

е5 = {2, 4}

е3 = {3, 4}

])

_Edges = {е1, е3, е2, e4, е5, е6}

_Head = table([

])

_Vertices={1,2,3,4} _Econnectivity = _Econnectivity _Vweight = table(sparse, [

])

_Countcuts = _Countcuts

_Edgelndex = table(symmetric, [

(2, 4) = {е5}

(1,2)={e1}

(1,4)={е2}

(3, 4) = {е3}

(2, 3) = {e4}

(1.3)={е6}

])

_Counttrees = _Counttrees _Status = {COMPLETE, SIMPLE} _Neighbors = table([

3={1,2,4} 4 ={1,2,3}

1 = {2, 3, 4}

2 ={1,3, 4}

]) „Tail = table([

])

])

Разумеется, приведенные примеры далеко не исчерпывают всех задач, которые можно решать с применением графов. Но они наглядно демонстрируют, что для большинства пользователей пакет network превращает графы из окутанного ореолом таинственности средства в простой рабочий инструмент.

12.10. Пакет числовой аппроксимации numapprox 12.10.1. Состав пакета numapprox

Этот пакет содержит небольшое число безусловно очень важных функций:

chebdeg chebmull chebpade chebsort chebyshev confracform hornerform infnorm laurent minimax pade remez taylor

В их числе функции интерполяции и аппроксимации полиномами Чебышева, рядом Тейлора, отношением полиномов (Паде-аппроксимация) и др. Все они широко применяются не только в фундаментальной математике, но и при решении многих прикладных задач. Рассмотрим их, начиная с функций аппроксимации аналитических зависимостей.

12.10.2. Разложение функции в ряд Лорана

Для разложения функции { в ряд Лорана с порядком п в окрестности точки с х=а (или х=0) служит функция:

laurent(f, х=а, п) или laurent(f, х, п)

Представленный ниже пример иллюстрирует реализацию разложения в ряд Лорана:

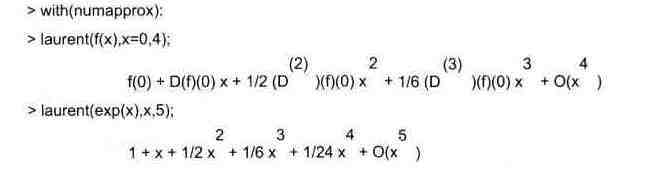
12.10.3. Паде-аппроксимация аналитических функций

Для аппроксимации аналитических функций одной из лучших является Паде-ап-проксимация, при которой заданная функция приближается отношением двух полиномов. Для осуществления такой аппроксимации используется функция

pade(f, x=a, [m,n]) или pade(f, x, [m,n])

Здесь: f — аналитическое выражение или функция, х — переменная, оть.к^итель-но которой записывается аппроксимирующая функция, а — координата точки, относительно которой выполняется аппроксимация, m, n — максимальные степени полиномов числителя и знаменателя.

Технику аппроксимации Паде поясняет рис. 12.5.

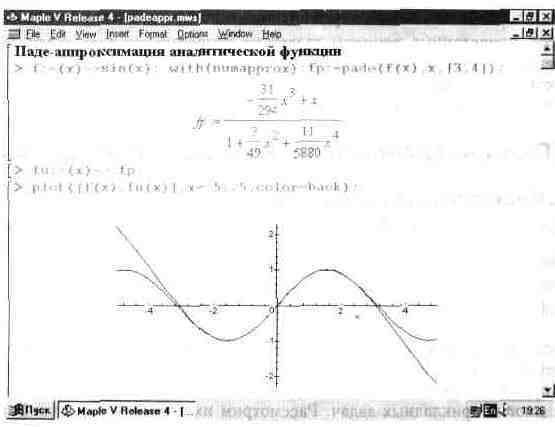
Рис. 12.5. Аппроксимация Паде для синусоидальной функции.

На рис. 12.5 представлена аппроксимация синусоидальной функции, а также построены графики этой функции и аппроксимирующей функции.

12.10.4. Паде-аппроксимация с полиномами Чебышева

Для многих аналитических зависимостей f хорошие результаты дает аппроксимация полиномами Чебышева. В общем случае применяется Паде-аппроксимация с отношением таких полиномов. Она реализуется функциями:

chebpade(f, x=a..b, [m,n]) chebpade(f, х, [m,n¦) chebpade(f, a..b, ¦m,n])

Здесь: a..b задает отрезок аппроксимации, тип — максимальные степени числителя и знаменателя полиномов Чебышева.

Приведенный ниже пример показывает аппроксимацию Паде полиномами Чебышева для функции f=cos(x):

>with(numapprox):

> chebpade(cos(x), x=0..1, 5);

.8235847380 Т(0, 2 х - 1) - .2322993716 Т(1, 2 х - 1)

- .05371511463 Т(2, 2 х- 1)+ .002458235267 Т(3, 2 х - 1)

-5 + .0002821190575 Т(4, 2 х- 1) - .7722229156 10 Т(5,2х-1)

> chebpade(cos(x), x=0..1, [2,3]);

(.8162435876 Т(0, 2 х- 1)- .1852356297 Т(1, 2 х- 1) -.05170917482Т(2,2х-1))/(Т(0,2х-1) +.06067214548 Т(1, 2 х-1)+ .01097466398 Т(2, 2 х - 1) + .0005311640964 Т(3, 2 х - 1))

12.10.5. Наилучшая минимаксная аппроксимация

Минимаксная аппроксимация отличается от Паде-аппроксимации минимизацией погрешностей в точках, где функция минимальна и максимальна. Она реализуется следующей функцией:

minimax(f, x=a..b, [m,n], w, 'maxerror') minimax(f, a..b, [m,n], w, 'maxerror')

Здесь, помимо уже отмеченных параметров, w — процедура или выражение specifying the weight function (no умолчанию 1), maxerror — переменная, которой приписывается значение minimax — нормы. Ниже дан пример аппроксимации функции cos(x) в интервале [-3,3]:

12.10.6. Наилучшая минимаксная аппроксимация по алгоритму Ремеза

Для получения наилучшей полиномиальной аппроксимации используется алгоритм Ремеза, который реализует следующая функция:

remez(w, f, a, b, m, n, crit, 'maxerror')

Здесь: w — процедура, представляющая функцию w(x) > 0 в интервале [a,b], f — процедура, представляющая аппроксимируемую функцию f(x), а и b — числа, задающие интервал аппроксимации [а,Ь], тип — степени числителя и знаменателя аппроксимирующей функции, crit — массив, индексированный от 1 .. m+n+2 и представляющий набор оценок в критических точках (т.е. точек максимума/минимума кривых огрешности), maxerror — имя переменной, которой присваивается минимаксная норма w*abs(f - г).

Следующий пример иллюстрирует применение данной функции для аппроксимации функции erf(x):

> with(numapprox):

> Digits:=12: w := proc(x) 1.0 end:

> f := proc(x) evalf(erf(x)) end:

>crit:=array(1..7,[0,.10,.25,.50,.75,.90,1.0]):

> remez(w,f,0,1,5,0,crit,'maxerror');

x -> .0000221268859 + (1.12678937622 + (.018447321427

+ (-.453446232258 + (.141246775408 + .00966355215462 x) x) x) x) x

> maxerror;

.0000221268881831

12.10.7. Другие функции пакета

Отметим назначение других функций пакета гштарргох:

chebdeg(p)	Возвращает степень полинома Чебышева р.
chebmult(p, q)	Умножает полиномы Чебышева р и q.
chebsort(e)	Сортирует элементы ряда Чебышева.
confracform(r)	Преобразует рациональное выражение г в цепную дробь.
confracform(r, x)	Преобразует рациональное выражение г в цепную дробь с независимой переменной x.
hornerform(r)	Преобразует рациональное выражение г в форму Горнера.
hornerform(r, x)	Преобразует рациональное выражение г в форму Горнера с независимой переменной x.
infnorm(f, x=a...b, 'xmax')	Возвращает L-бесконечную норму функции на отрезке х [а,Ь¦.
infnorm(f, a...b, 'xmax')	Возвращает L-бесконечную норму функции на отрезке ¦а,Ь].

12.11. Пакет ортогональных полиномов orthopoly

Ортогональные полиномы находят самое широкое применение в различных математических расчетах. В пакете orthopoly задано 6 функций:

G H LPT U

Однобуквенные имена этих функций отождествляются с первой буквой в наименовании ортогональных полиномов. Вопреки принятым в Maple V правилам, прописные буквы в названии этих полиномов не указывают на инертность данных функций — все они являются немедленно вычисляемыми. Функции данного пакета будут полностью описаны в этой главе.

Отметим определения указанных функций:

G(n,a,x) — полином Гегенбауэра (из семейства ультрасферических полиномов);

Н(п,х) — полином Эрмита;

L(n,x) — полином Лагерра;

L(n,a,x) — обобщенный полином Лагерра;

Р(п,х) — полином Лежандра;

P(n,a,b,x) — полином Якоби;

T(n,x) — обобщенный полином Чебышева первого рода;

U(n,x) — обобщенный полином Чебышева второго рода.

Свойства ортогональных многочленов хорошо известны ([43]). Все полиномы (у нас их называют также многочленами) характеризуются целочисленным порядком п, аргументом х и иногда дополнительными параметрами а и Ь. Существуют простые рекуррентные формулы, позволяющие найти полином п-го порядка по значению полинома (п-1)-го порядка. Эти формулы и используются для вычисления полиномов высшего порядка.

Ниже даны примеры вычисления ортогональных полиномов:

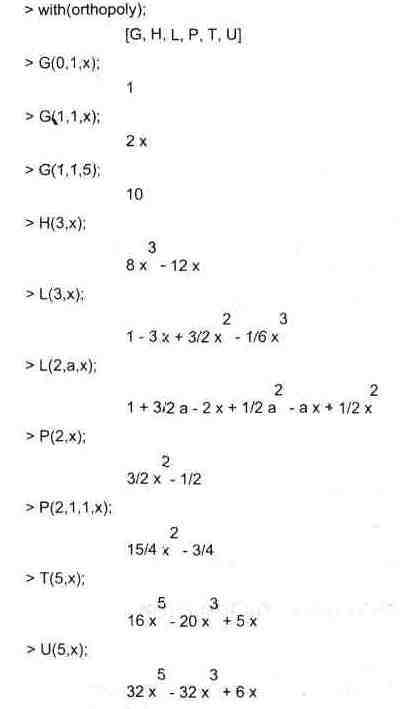
12.12. Пакеты функций расширенной графики plots и plottools

Это, несомненно, один из самых мощных пакетов, который заинтересует любого пользователя. Он предоставляет расширенные возможности двумерной и трехмерной графики, а также почти все мыслимые средства графического представления математических понятий и функций. В пакете имеется 49 функций графики:

animate animate3d changecoords complexplot complexplot3d conformal contourplot contourplot3d coordplot coordplot3d cylinderplot densityplot display display3d fieldplot fieldplotSd gradplot gradplot3d implicitplot i mplicitplot3d inequal listcontplot listcontplot3d listdensityplot listplot

listplot3d loglogplot logplot matrixplot odeplot

pareto pointplot pointplot3d polarplot polygonplot

polygonplot3d polyhedraplot replot rootlocus semilogplot

setoptions setoptions3d spacecurve sparsematrixplot sphereplot

surfdata textplot textplot3d tubeplot

Этот пакет настолько важен, что избранным его функциям посвящена глава 13.

Пакет plottools служит для создания различных графических примитивов — дуг, окружностей, эллипсов, цилиндров и т.д. Он используется в графических структурах, описанных в главе 13. Возможности пакета реализуются в функциях:

plottools[function](args) или function(args)

Указанные функции создают базовые графические объекты, которые выводятся на экран дисплея с помощью функции plots[display].

Пакет plottools задает построение следующих базовых графических объектов:

arc arrow circle cone cuboid curve cutin cutout cylinder disk dodecahedron ellipse ellipticArc hemisphere hexahedron hyperbola icosahedron line octahedron pieslice point polygon rectangle semitorus sphere tetrahedron torus

После создания графической структуры возможно применение следующих функций:

rotate scale stellate transform translate

Возможности пакета plottools будут более детально рассмотрены в главе 13.

12.13. Пакет реализации степенных разложений powseries

Степенные разложения часто используются в математических расчетах для приближенного представления разнообразных функций и обеспечения единообразия их представления. В пакете powseries сосредоточены расширенные средства по реализации таких разложению. Они представлены 22 функциями:

compose evalpow inverse multconst multiply negative powadd powcos powcreate powdiff powexp powint powlog powpoly powseries powsin powsolve powsqrt quotient reversion subtract tpsform

В пакете powseries имеется целый ряд функций для работы со степенными рядами:

	Объединяет ряды а и b.
Epose (a,b) oow(expr)	Вычисляет выражение ехрг и возвращает его в виде ряда.
inverse(p)	Инвертирует ряд р.

multconst(p,const)	Умножает ряд р на константу const.
multiply(a,b)	Умножает ряд а на ряд Ь.
negative(p)	Возвращает аддитивный обратный по отношению к b ряд.
powadd(a,b,...)	Складывает ряды а, b,... .
powcreate(expr)	Создает ряд для выражения ехрг.
powpoly(pol,var)	Создает ряд для полинома ро1 по переменной var.
powsolve(sys)	Создает ряд для решения дифференциальных уравнений sys.
¦ quotient(a,b)	Возвращает результат деления а на b в виде ряда.
reversion(a)	Дает обратное к композиции разложение ряда а.
subtract(a.b)	Дает разность рядов а и b.

В выражении ехрг могут использоваться операторы: +,-,*,/,'. С ними могут комбинироваться встроенные функции и функции пользователя, например f(g). Кроме того могут использоваться следующие функции:

powexp powinv powlog powneg powrev powdiff powint powquo powsub powcos powtan powsec powcsc powcot powsinh powcosh powtanh powsech powcsch powcoth powsqrt powadd multiply

Назначение большинства их этих функции очевидно из их названия: они возвращают соответствующую функцию (указанную после слова pow в имени) в виде разложения в ряд или полинома. Например, powexp раскладывает выражения с экспоненциальными функциями в ряд.

Получаемые функциями ряды представляются в специальном формате. Поэтому для их применения в обычном виде необходимо использовать функцию tpsform в виде:

tpsform(p, var, order) — преобразует ряд р;

tpsform(p, var) — преобразует.

Здесь: р — имя степенного ряда, var — переменная, относительно которой записан ряд, order — порядок ряда. Если параметр order не указан, используется значение глобальной переменной Order.

Ниже даны примеры, иллюстрирующие технику работы со степенными разложе-ниями:

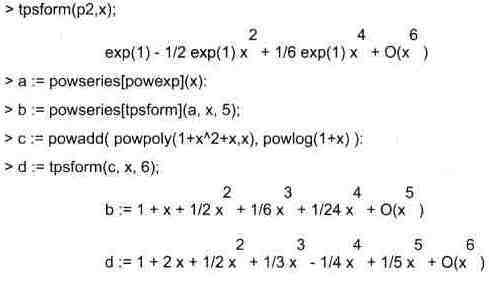
12.14. Пакет для решения задач линейной оптимизации simplex

Задачи линейной оптимизации важны как в фундаментальных, так и в прикладных приложениях математики. В пакете simplex дан достаточно представительный набор функций и определений для решения таких задач:

NONNEGATIVE basis convexhull cterm define_zero

display dual equality feasible maximize

minimize pivot pivoteqn pivotvar ratio

setup standardize

Отметим назначение этих функции:

NONNEGATIVE	Ключевое слово, указывающее на неотрицательный тип данных.
basis	Возврат списка основных переменных для множества линейных уравнении.
convexhull	Вычисление выпуклой оболочки для набора точек.
cterm	Задание констант для системы уравнений или неравенств.
definezero	Определение наименьшего значения, принимаемого за ноль (по умолчанию оно увязано со значением системной переменной Digits).
display	Вывод в матричной форме системы уравнений или неравенств.
dual	Выдача сопряженных выражений.
equality	Опция для функции convert, указывающая на эквивалентность.
feasible	Выяснение возможности решения заданной задачи.
maximize	Вычисление максимума функции.
mnimize	Вычисление минимума функции.
pivot	Создание новой системы уравнений с заданным главным элементом.
pivoteqn	Выдача подсистемы уравнений для заданного главного элемента.
pivotvar	Выдача переменных с положительными кочффициентами в целевой функции.
ratio	Выдача отношений для определения наиболее жесткого ограничения.
setup	Задание системы линейных уравнений.
standardize	Приведение заданной системы уравнений или неравенств к стандартной форме.

Главными из этих функций являются функции maximize и minimize, оптимизирующие задачу симплекс-методом. Они записываются в следующей форме:

maximize(f, С)

minimize(f, С)

maximize(f, С, vartype)

minirnize(f, С, vartype)

maximize(f, С, vartype, 'NewC', 'transform')

minimize(f, C, vartype, 'NewC', 'transform').

Здесь: f — линейное выражение, С — множество или лист условии, vartype — задаваемый лпционно тип переменных NONNEGATIVE или UNRESTRICTED, NewC и transform — имена переменных, которым присваиваются соответственно оптимальное описание и переменные преобразования. Ниже даны примеры применения этих функций:

> with(simplex):

Warning, new definition for maximize Warning, new definition for minimize

> minimize( x-y, {4«x+2»y <= 10, 3*x+4*y <= 16}, NONNEGATIVE.'NC'.'vf );

{x = 0, у = 4}

> NC;vt;

{у = - 1/4 _SL2 +4-3/4 x, _SL1 = 2 - 5/2 x + 1/2 _SL2}

{} > maximize( x+y, {4tx+2«y <= 10, З'х+4'у <= 16}, NONNEGATIVE );

{у= 17/5,х=4/5}

12.15. Пакет статистических расчетов stats 12.15.1. Характеристика пакета stats

Мир математических систем сейчас насыщен статистическими системами, например, такими, как Statistica или StatGraphics. Они прекрасно приспособлены для решения задач статистической обработки обширных массивов данных. Тем не менее проведение статистических расчетов в системе Maple V возможно и в ряде случаев весьма целесообразно, например, когда они являются частью исследовательского проекта.

Пакет stats для таких расчетов представлен всего двумя многоцелевыми статистическими функциями:

stats[subpackage, functionj(args) subpackage[function](args)

Однако, благодаря специальной форме задания параметров (в частности, в виде субпакетов subpackages), возможно вычисление самых разнообразных статистических функций. Возможно обращение к следующим субпакетам:

anova — дисперсионный анализ;

describe — функции распределения вероятности;

fit — линейная регрессия;

random — генерация случайных чисел с различными законами распределения;

statevalf — вычисление статистических функций и получение оценок для массивов данных;

statplots — построение графиков статистических функций;

transform — функции преобразования данных.

12.15.2. Генерация случайных чисел с заданным распределением

Основой этого подпакета является функция random:

randomfdestribution] (quantity,uniform,method)

или

stats[random, destribution] (quantity,uniform, method),

где:

destribution — описание закона распределения случайных чисел;

quantity — положительное число, указывающее на количество получаемых

случайных чисел (по умолчанию 1, возможна опция 'generator');

uniform — процедура генерации чисел с равномерным распределением

или ключевое слово 'default' (по умолчанию);

method — указание на один из трех методов ('auto', 'inverse' или 'builtin').

Возможно задание дискретных и непрерывных распределений, например, bino-miald — дискретное биномиальное распределение, discreteuniform — дискретное равномерное распределение, empirical — дискретное эмпирическое распределение, poisson — дискретное распределение Пуассона, beta — бета-распределение, cauchi — распределение Коши, exponential — экспоненциальное отношение и др. (практически существуют функции для всех известных распределений).

Следующие примеры демонстрируют технику получения случайных чисел с заданным законом распределения:

> with(stats):Digits:=5:

> stats[random, normald](5);

.79697, -.40654, -.085304, .71297, 1.1119 > stats[random, normald](5, 'default', 'inverse');

-.63631, .72218, -.063423, -1.5123, .84664 > seed:=1:

> uniform_generator:=proc(.) > global seed;

> seed:=irem(seed*11,101);

>RETURN(seed/101) ' . > end:

> random[gamma[3]](5,uniform_ge,nerator);

1.1719, 1.5144,3.3684, 1.9976,4.8183

12.15.3. Регрессионный анализ

Под регрессионным анализом (или просто регрессией) обычно подразумевают нахождение некоторой формальной аналитической зависимости, которая приближенно (по критерию минимума среднеквадратичной ошибки) аппроксимирует

некоторую исходную зависимость. Чаще всего она бывает представлена набором (облаком) точек, например, данных эксперимента.

Для проведения регрессионного анализа служит функция fit, которая вызывается следующим образом:

stats[fit,leastsquare[vars,eqn,parms]](data)

или

fit[leastsquare[vars,eqn,parms]](data)

где: data — список данных, vars — список переменных для представления данных, eqn — уравнение, задающее аппроксимирующую зависимость (по умолчанию линейную), parms — множество параметров, которые будут заменены вычисленными значениями.

На примерах ниже показано проведение регрессии с помощью функции fit для зависимостей вида у(х):

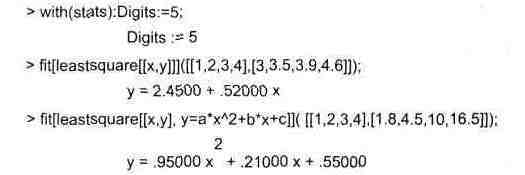
В первом примере функция регрессии не задана, поэтому реализуется простейшая линейная регрессия и функция fit возвращает полученное уравнение регрессии для исходных данных, представленных списками координат узловых точек. Это уравнение аппроксимирует данные с наименьшей среднеквадратичной погрешностью. Во втором примере задано приближение исходных данных степенным многочленом второго порядка. Вообще говоря, функция fit обеспечивает приближение любой функцией и, таким образом, реализует практически все виды регрессии для функций одной переменной.

Однако функция fit может обеспечивать регрессию и для функций ряда переменных. При этом просто надо увеличить размерность массивов исходных данных. В качестве примера ниже приведен пример регрессии для функции двух переменных

>f:=fit[leastsquare[[x,y,z],z=a+b*x+c*y,{a,b,c}]]\

([[1,2,3,5,5],[2,4,6,8,8],[3,5,7,10,Weight(15,2)]]);

f:=z=1 +13/3 х-7/6 у

> fa:=unapply(rhs(f),x,y);

fa := (x, у)-> 1 + 13/3 х-7/6 у >fa(1.,2.);

2.999999999 > fa(2,3);

37/6

В данном случае уравнение регрессии задано в виде г=а+Ь*х+с*у. Обратите внимание на важный момент в конце этого примера — применение полученной функции регрессии для вычислений или построения ее графика. Прямое приме-

нение функции / в данном случае невозможно, так как она представлена в невычисляемом формате. Для получения вычисляемого формата она преобразуется в функцию двух переменных }а(х.,у) путем отделения правой части в выражении для функции /. После этого возможно вычисление значении функции fa(x,y) для любых заданных значений х и у.

12.16. Пакет полезных студентам функций — student

В этом пакете имеется почти полсотни функций:

D	Дифференциальный оператор.
Diff	Инертная форма функции вычисления производной.
Doubleint	Инертная форма функции вычисления двойного интеграла.
Int	Инертная форма функции интегрирования int.
Limit	Инертная форма функции вычисления предела limit.
Lineint	Инертная форма функции вычисления линейного интеграла lineint.
Point	Тестирование объекта на соответствие типу точки (point).
Product	Инертная форма функции вычисления произведения членов последовательности.
Sum	Инертная форма функции вычисления суммы членов последовательности.
Tripleint	Инертная форма функции вычисления тройного интеграла.
changevar	Замена переменной.
combine	Объединение подобных членов.
completesquare	Вычисление полного квадрата (многочлена).
distance	Вычисление расстояния между точками.
equate	Создание системы уравнений из списков, таблиц, массивов.
extrema	Вычисление экстремума выражения.
integrand	Вывод подынтегрального выражения из-под знака инертного интеграла.
intercept	Нахождение точки пересечения двух кривых.
intparts	Интегрирование по частями.
isolate	Выделение подвыражения.
leftbox	Графическая иллюстрация интегрирования методом левых прямоугольников.
leftsum	Числовое приближение к интегралу левыми прямоугольниками.
makeproc	Преобразование выражения в процедуру Maple.
maximize	Вычисление максимума функции.
middlebox	Графическая иллюстрация интегрирования методом центральных прямоугольников.
middlesum	Числовое приближение к интегралу центральными прямоугольниками.
midpoint	Вычисляет среднюю точку сегмента линии.
minimize	Вычисление минимума функции.
powsubs	Подстановка для множителей выражения.
rightbox	Графическая иллюстрация интегрирования методом правых прямоугольников.
rightsum	Числовое приближение к интегралу правыми прямоугольниками.

showtangent	График функции и касательную линию.
simpson	Числовое приближение к интегралу по методу Симпсона.
slope	Вычисление и построение касательной к заданной точке функции.
trapezoid	Числовое приближение к интегралу методом трапеции.
value	Вычисляет инертные функции.

Это, несомненно, один из самых «милых» для студентов и аспирантов пакетов. В нем собраны наиболее распространенные и нужные функции, которые студенты университетов и иных вузов обычно используют на практических занятиях, при подготовке курсовых и дипломных проектов. Набор этих функции, разумеется, не ограничивается «скромными» потребностями студентов — просто это наиболее распространенные функции, в основном относящиеся к математическому анализу. Наряду со студентами эти функции широко используют профессионалы-математики и ученые, использующие математические методы в своей работе.

В пакетах расширения Maple V можно найти множество специальных функции для вычисления интегралов различного типа. Например, в пакете student имеются следующие функции:

Int(expr,x) — инертная форма вычисления неопределенного

интеграла;

Doubleint(expr,x,y,Domain) — вычисление двойного интеграла по переменным

х и у по области Domain;

Tnpleint(expr,x,y,z) — вычисление тройного интеграла;

intparts(f,u) — интегрирование по частям.

На рис. 12.6 показано применение функции Tripleint этого пакета для вычисления тройного интеграла.

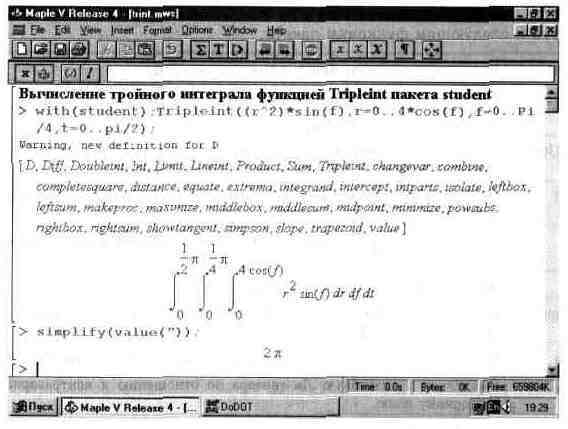
Рис. 12.6. Вычисление тройного интеграла с помощью функции Tripleint.

В главе 13 будет описано несколько графических функции пакета student, указанных выше в их общем списке. Они в основном используются для иллюстрации интегрирования методом прямоугольников и построения касательной к заданной точке функции. Пакет дает также дополнительные возможности по анализу функций, например по поиску экстремумов функций.

12.17. Пакет работы с тензорами tensor

Этот новый пакет, отсутствовавший в предшествующих реализациях Maple V, дает средства для работы с тензорами и вычислениями, используемыми в общей теории относительности. В нем использован специальный тип данных tensor_type в виде таблиц с двумя полями: компонент и характеристик индексов. Поле компонент — массив с размерностью, эквивалентной рангу объекта. Поле характеристик индексов задается списком чисел 1 и -1. При этом 1 на i-й означает, что соответствующий индекс контрвариантный, а - 1 — что он ковариантный.

Процедура tensor_type вовзращает логическое значение true, если ее первый аргумент удовлетворяет свойствам тензора, и false, если он этому свойству не удовлетворяет.

Каждому тензору соответствуют еще две таблицы. Таблица коэффициентов вращения задает коэффициенты вращения Ньюмена-Пенроуса, которые вычисляются функцией tensor[npspin] и индексируются именами греческих букв alpha, beta, gamma, epsilon и т.д. Другая таблица (компонент кривизны) содержит компоненты кривизны Ньюмена-Пенроуса. Они представлены тремя полями:

полем Phi в виде массива размерности (0..2,0..2) с компонентами Риччи, поле Psi с массивом размерности (0..4) с компонентами Вейля и поле R со скаляром Риччи.

Объявление > with(tensor);

дает доступ к следующим функциям пакета:

Christoffell	Вычисление символов Кристоффеля первого рода.
Christoffel2	Вычисление символов Кристоффеля второго рода.
Einstein	Возвращает тензор Эйнштейна.
displayalJGR	Описывает ненулевые компоненты всех тензоров и параметров, вы численных командой tensorsGR (Общая теория относительности).
displayGR	Описывает ненулевые компоненты конкретного тензора (Общая теория относительности).
enorsGR	Вычисляет тензор кривизны в данной системе координат (Общая теория относительности).
Jacobian	Якобиан преобразования координат.
Killingeqns	Вычисляет компоненты для уравнений Киллинга (имеет отношение к симметриям пространства).
LeviCivita	Вычисляет ковариантные и контравариантные псевдотензоры Леви-Чивита.
Liedin	Вычисляет производную Ли тензора по отношению к контравариантному векторному полю.
Ricci	Тензор Риччи.
Ricciscalar	Скаляр Риччи.

Riemann	Тензор Римана.
RiemannF	Тензор кривизны Римана в жесткой системе отсчета.
Weyl	Тензор Веиля.
act	Применяет операции к элементам тензора, таблицам вращении или кривизны.
antisymmetrize	Антисимметризация тензора по любым индексам.
change basis	Преобразование системы координат.
commutator	Коммутатор двух контравариантных векторных полей.
compare	Сравнивает два тензора, .таблицы вращении или кривизны.
conj	Комплексное сопряжение.
connexF	Вычисляет связующие коэффициенты для жесткой системы координат.
contract	Свертка тензора по парам индексов.
convertNP	Преобразует связующие коэффициенты или тензор Римана к формализму Ньюмена-Пенроуза.
covdiff	Ковариантное дифференцирование.
create	Создает тензорный объект.
dimetric	Первая частная производная метрики.
d2metric	Вторая частная производная метрики.
directionaLdiff	Производная по направлению.
dual	Осуществляет дуэльную операцию над индексами тензора.
entermetric	Обеспечивает ввод пользователем координатных переменных и ковариант-ных компонент метрического тензора.
exteriordifF	Внешнее дифференцирование полностью антисимметричного ковариантного тензора.
exteriorprod	Внешнее произведение двух ковариантных антисимметричных тензоров.
frame	Задает систему координат, которая переводит метрические компоненты к диагональной сигнатурной матрице (с положительными или отрицательными единицами).
geodesiceqns	Уравнение Эйлера-Лагранжа для геодезических кривых.
getchar	Возвращает признак (ковариантный/контравариантный) объекта.
getcompts	Возвращает компоненты объекта.
getrank	Возвращает ранг объекта.
invars	Инварианты тензора кривизны Римана (Общая теория относительности).
invert	Обращение тензора второго ранга. .
lincom	Линейная комбинация тензорных объектов.
lower	Опускает индексы.
npcurve	Компонента кривизны Ньюмена-Пенроуза в формализме Дебевера (Общая теория относительности).
npspin	Компонента вращения Ньюмена-Пенроуза в формализме Дебевера (Общая теория относительности).
partiaLdiff	Частная производная тензора.
permuteindices	Перестановка индексов.

petrov	Классификация Петрова тензора Веиля.
prod	Внутреннее и внешнее тензорное произведение.
raise	Поднятие индекса.
symmetrize	Симметризация тензора по любым индексам.
transform	Преобразование системы координат.

Примеры применения этого пакета можно найти в справочной базе данных системы. Пакет представляет интерес для физиков-теоретиков, работающих в области Общей теории относительности и в ее приложениях. Для них (но не для большинства пользователей) приведенные данные полезны и понятны.

12.18. Пакет упорядочения переменных totorder

Этот небольшой пакет служит для упорядочения переменных по заданным неравенствам г и содержит следующие функции:

tassume tis forget ordering init Приведем их определения (г — последовательность отношений):

tasume(r)	Дает полное упорядочение имен по заданной последовательности отношении.
tis(r)	Тестирует неравенства.
forget(r)	Уничтожает отношения порядка для одной переменной.
forget(everything)	Уничтожает отношения порядка для всех переменных.
orderingO	Возвращает текущие отношения порядка.
initO	Восстанавливает первоначальные отношения порядка.

Примеры применения функций пакета totorder:

> with(totorder):init():tassume(x<y, y<z, z=d);

assumed, x<y,y<z,z=d > tassume(u>d);

assumed, d < u > tis(u<z);

false > forget(u);

forgotten, u

> orderingO;

x<y,y<d,d=z > tassume(u>d);

assumed, d < u > tis(2"z-z<d);

false

> tis(2*z-z=d);

true

12.19. Пакеты специального назначения

В этом разделе дано перечисление функций и указано назначение ряда пакетов

специального назначения, относящихся к теории чисел, формам и иным специальным разделам математики, редко используемым в прикладных расчетах.

12.19.1. Пакет Domains

Этот пакет служит для создания доменов — таблиц операции для вычислений.

Ограничимся приведением вариантов задания функции Domains этого пакета:

Domains[domain¦ Domains[evaldomainsj Dornains[example] Domainslcoding]

Следующий пример поясняет создание и использование доменов Q (для рациональных данных) и Z (для целочисленных данных):

> with(Domains);

—„—————— Domains version 1.0 ————————

Initially defined domains are Z and Q the integers and rationals Abbreviations, e.g. DUP for DenseUnivariatePolynomial, also made [init]

>Q['+'](1/2,2/5,3/8);

51

40 >Z[Gcd](660,130);

10

Следующая операция показывает, что домен Z является таблицей:

> type(Z.table);

true

А функция show позволяет вывести полный перечень всех операций, доступных для домена Z:

> show(Z,operations);

Signatures for constructor Z note: operations prefixed by — are not available

-: (Integer.Z) -> Z t:(Z,Z")-> Z + : (Z,Z*) -> Z

-: (Z,Z) -> Z

-: Z -> Z

o:z

1 :Z

< : (Z,Z) -> Boolean <= : (Z,Z) -> Boolean <> : (Z,Z) -> Boolean = : (Z,Z) -> Boolean > : (Z,Z) -> Boolean >= : (Z,Z) -> Boolean Abs : Z -> Z

Characteristic : Integer Coerce : Integer -> Z

Div : (Z,Z) -> Union(Z.FAIL) EuclideanNorm : Z-> Integer Factor: Z -> [Z,[[Z,lnteger]']] Gcd : Z* -> Z

Gcdex : (Z.Z.Name) -> Z Gcdex : (Z,Z,Name,Name) -> Z Input: Expression -> Union(Z,FAIL) Inv : Z -> Union(Z,FAIL) Lcm : Z- -> Z Max : (Z.Z*) -> Z Min : (Z.Z*) -> Z Modp : (Z,Z) -> Z Mods : (Z,Z) -> Z

ModularHomomorphism : () -> (Z -> Z,Z) Normal: Z -> Z Output: Z -> Expression Powmod : (Z.lnteger.Z) -> Z Prime : Z -> Boolean Quo : (Z.Z.Name) -> Z Quo : (Z,Z) -> Z Random : () -> Z

RelativelyPrime : (Z,Z) -> Boolean Rem : (Z,Z) -> Z Rem : (Z.Z.Name) -> Z Sign :Z->UNION(1, -1,0) SmallerEuclideanNorm : (2,Z) -> Boolean Sqrfree : Z -> [Z,[[Z,lnteger]']] Type : Expression -> Boolean Unit: Z -> Z

UnitNormal: Z -> [Z,Z,Z] Zero : Z -> Boolean л : (Z.lnteger) -> Z

Домены позволяют передавать в качестве параметра процедур набор функций в виде единого целого, что и объясняет название этих объектов. Предполагается, что это может привести к заметному сокращению кодов программ вычислении в

будущих реализациях системы Maple. Пока же возможности доменов скорее выглядят как очередная «экзотика», чем как реальное средство для оптимизации

вычислении. Потребуется время, чтобы показать, что это не так.

12.19.2. Пакет функций теории чисел numtheory

В этом обширном пакете собрано 58 функции, относящихся к теории чисел:

В F GIgcd J L М bernoulli bigomega cfrac cfracpol cyclotomic divisors euler factorEQ factorset fermat ifactor [factors imagunit index invcfrac invphi isolve isprime issqrfree ithprime jacobi kronecker lambda legendre mcombine mersenne minkowski mipolys mlog mobius mroot msqrt nearest? nextprime nthconver nthdenom nthnumer nthpow order

pdexpand phi pprimroot prevprime primroot

quadres rootsunity ' safeprime sigma sq2factor

sum2sqr tau thue

Большинство функции этого пакета достаточно просты, и заинтересованный читатель вполне в состоянии провести их тестирование самостоятельно.

12.19.3. Пакет ра<Лсдля работы с р-адическими числами

Этот весьма специфический пакет содержит следующие функции для работы с р-адическими числами:

evalp expansion function Icoeffp orderp ordp ratvaluep rootp valuep

Ввиду специфичности функций этого пакета их изучение мы оставляем заинтересованному читателю.

12.19.4. Пакет для определения конечного поля Галуа GF

Этот пакет содержит функцию GF в двух формах:

GF(p,k) и GF(p,k,a)

Здесь: р — простое число, к — натуральное число, а — неприводимый полином степени k над полем целых чисел по модулю. Функция GF возвращает таблицу G-функций и констант для выполнения арифметических операций над конечным полем GF(pk), именуемым полем Uakkef с pk-элементами.

12.19.5. Пакет GausslntArm работы с Гауссовыми целыми числами

Гауссово целое число — число вида а+1*Ь, где а и b — любые целые рациональные числа. Так что их можно считать подвидом более общего класса комплексных чисел. Пакет Gaussint содержит достаточно представительный набор функций для работы с такими числами:

GIbasis GIchrem Oldivisor GItacpoly GIfacset GIfactor GIfactors GIgcd GIgcdex GIhermite Glissqr GIlcm GImcmbine GInearest GInodiv GInorm GInormal GIorder GIphi GIprime GIquadres GIquo . GIrem GIroots GIsieve GIsmith GIsqrfree GIsqrt Glunitnormal

Нетрудно заметить, что в этот набор входят уже известные числовые функции к чьим именам добавлены буквы GI. Например, функция GIfactor(c) раскладывает Гауссово число на простые множители, GIgcd(cl,c2) находит наибольший общий делитель Гауссовых чисел с1 и с2 и т.д. Функции этого пакета достаточно просты, так что ограничимся приведенными примерами. Гауссовы целые числа в большинстве научно-технических расчетов встречаются крайне редко. Так что этот пакет рассчитан на специалистов-математиков, работающих в области теории чисел.

areconjugate center centralizer convert core

cosets cosrep derived grelgroup groupmember

grouporder inter invperm isabelian isnormal

issubgroup mulperms normalizer orbit permgroup

permrep pres subgrel typ

В рамках основной ориентации данной книги — массовые математические и научно-технические расчеты — применение этих функций довольно ограничено. Надо полагать, специалисты в этой области смогут разобраться с этим пакетом самостоятельно.

12.19.11. Пакет для работы с симметрией Ли liesymm

В этом пакете, относящемся к понятиям симметрии Ли, имеется ряд функций:

&" &mod Eta Lie Lrank TD annul autosimp close d depvars determine dvalue extvars getcoeff getform hasclosure hook indepvars makeforms mixpar prolong reduce setup translate vfix wcollect wdegree wedgeset wsubs

Эти функции представляют достаточно специфический интерес и потому в дальнейшем не рассматриваются.

12.19.12. Пакет работы с суммами sumtools

Этот инструментальный пакет предназначен для работы с суммами. Он содержит указанные ниже функции:

Hypersum Sumtohyper extended_gosper gosper hyperrecursion hypersum hyperterm simpcomb sumrecursion sumtohyper

12.19.13. Пакет организации мультипроцессов process

Этот узкоспециализированный пакет содержит ряд функций по организации мультипроцессов:

block exec fork kill pclose pipe popen wait

Данные функции представляют интерес для пользователей операционной системы UNIX, так что в проблематику данной книги не входят.

12.20. Библиотека пользователей SHARE

В поставку системы Maple V R4 Power Edition входит богатая библиотека расширений, составленная пользователями этой системы. Она может быть получена и по Internet. Сейчас эта библиотека имеет множество разделов, многие из которых подобны названиям пакетов расширений системы:

Раздел	Справка	Раздел	Справка
Algebra	?share,algebra	Modular computations	?share,mod
Analysis	?share,analysis	Numerics	?share,numerics
Calculus	?share,calculus	Number Theory	?share,numtheor
Combinatorics	?share,combinat	Graphics	?share,graphics
Conversions	?share,convert	Programming	?share,program
Courses	?share,courses	Science	?share, science
Engineering	?share,engineer	Statistics	?share,stats
Geometry	?share, geometry	System Tools	?share,system
Linear Algebra	?share,linalg

Для загрузки библиотеки совместного использования надо в командной строке дать команду

> with(share);

В состав большинства файлов библиотеки входит документация, подготовленная на языке LaTeX. Благодаря библиотеке share пользователи в разных странах мира могут работать над совместными проектами. В новой реализации Maple V R5 библиотека SHARE существенно расширена и поставляется на отдельном CD-ROM.