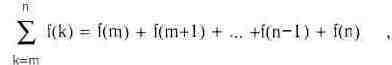
Вычисление сумм рядов
167
Глава 10. Операции и функции
математического анализа
10.1. Вычисление сумм рядов
Применение систем символьной математики особенно эффектно при решении задач математического анализа. Начнем рассмотрение таких операций с вычисления сумм. Вычисление суммы членов некоторой последовательности f(k) при изменении целочисленного индекса k от значения m до значения п с шагом +1, т.е. выражения
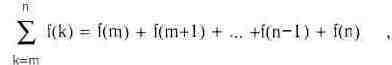
является достаточно распространенной операцией математического анализа. Для вычисляемой и инертной форм вычисления сумм служат следующие функции:
sum(f,k) suni(f,k=m..n) sum(f,k=alpha) Sum(f,k) Sum(t,k=m..n) Sum(f,k=alpha)
где: f — функция, задающая члены суммируемого ряда, k — индекс суммирования, тип — целочисленные пределы изменения k, alpha — RootOf-выражение. Значение п может приниматься бесконечным, тогда для п используется константа infinity.

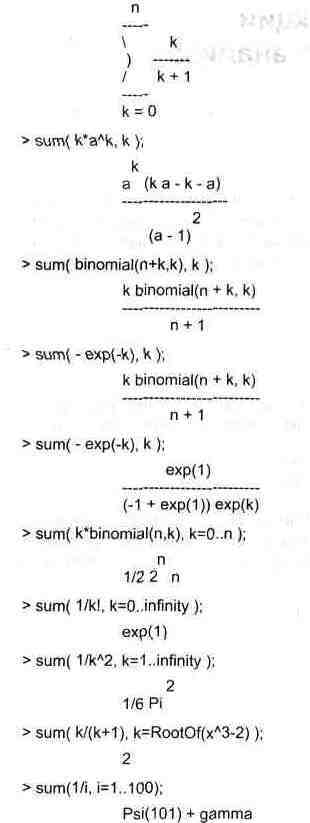
Многие бесконечные суммы сходятся к определенным численным или символьным значениям, и Maple V способен их вычислять. Это поясняют следующие примеры:
> Sum(1/i''2,i=1 ..infinity)=sum(1/i"2, i=1 ..infinity);
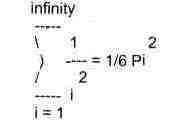

Как видно из приведенных примеров, средства вычисления сумм Maple V позволяют получать как численные значения сумм, так и аналитические — в том числе представляемые специальными математическими функциями. Дополнительные возможности по работе с суммами обеспечивает инструментальный пакет sum-tools, описанный в главе 12.
10.2. Вычисление произведений
Аналогичным образом для произведений членов f(i) некоторой последовательности, например вида
п
Y[ f(m)*f(m+l)*f(m+2)*...*f(n-l)*f(n)
i=m
используются следующие функции:
product(f,k) product(f,k=m..n) product(f,k=a]pha) Product(f,k) Product([,k=m..n) Product(t,k=alpha)
Обозначения параметров этих функций и их назначение соответствуют приведенным для функций вычисления сумм.
Примеры применения функций вычисления произведений даны ниже:
> product( ^2, k=1..4 );
576 > product( ^2, k );
2
GAMMA(k )
> product( a[k], k=1..4 );
a[1] a[2] a[3] a[4] >f:=[1,2,3,4,5];
f:=[1,2,3,4,5]
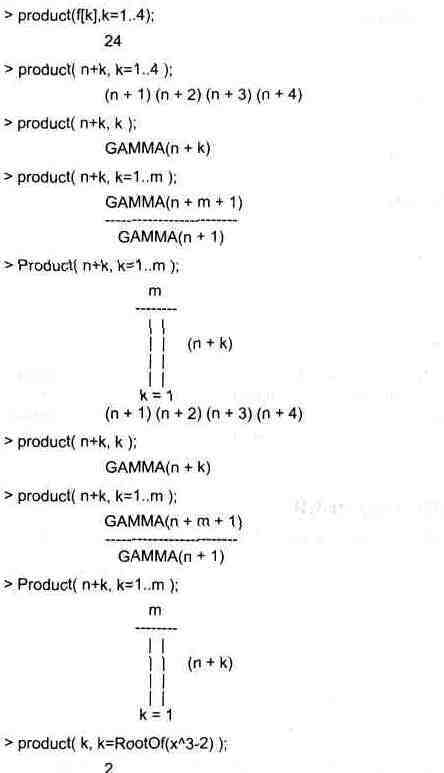
Как и в случае вычисления сумм, вычисление произведений возможно как в численной, так и в аналитической форме — разумеется, если таковая существует. Это показывает следующий пример:
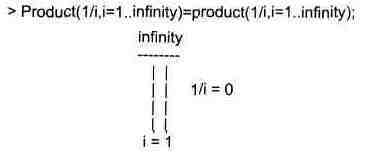
Нетрудно понять, что при i, стремящемся к бесконечности, перемножаемые члены ряда стремятся к нулю, а потому к нулю стремится и их произведение.
Вычисление производных 171
10.3. Вычисление производных 10.3.1. Функции дифференцирования выражений diff и Diff
Вычисление производных функции /"Ос) = df"(x) /dx" n- то порядка — одна из самых распространенных задач математического анализа. Для ее реализации Maple V имеет следующие основные функции:
diff(a, xl, х2, .... xn) diff(a, [xl, х2, ..., хп]) Diff(a, xl, х2, ..., хп) Diff(a, ¦xl, х2, .... xn])
Здесь а — дифференцируемое алгебраическое выражение, в частности, функция f(xl, х2, ..., xn) ряда переменных, по которым производится дифференцирование. Функция Diff является инертной формой вычисляемой функции diff и может использоваться для естественного воспроизведения производных в документах.
Первая из этих функций (в вычисляемой и в инертной форме) вычисляет частные производные для выражения а по переменным xl, х2, ..., xn. В простейшем случае diff(f(x),x) вычисляет первую производную функции f(x) по переменной х. При n большем 1 вычисления производных выполняются рекурсивно, например, diff(f(x), х, у) эквивалентно diff(diff (f(x), х), у). Оператор $ можно использовать для вычисления производных высокого порядка. Для этого после имени соответствующей переменной ставится этот оператор и указывается порядок производной. Например, выражение diff(f(x),x$4) вычисляет производную 4-го порядка и эквивалентно записи diff(f(x),x,x,x,x). A diff(g(x,y),x$2,y$3) эквивалентно diff(g(x,y),x,x,y,y,y).
Примеры вычисления производных:

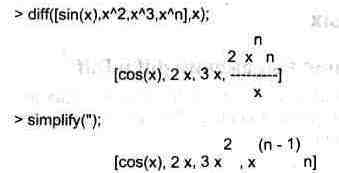
Как видно из приведенных примеров, функции вычисления производных могут использоваться с параметрами, заданными списками. Приведенные ниже примеры показывают эти возможности и иллюстрируют дифференцирование функции пользователя для двух переменных:
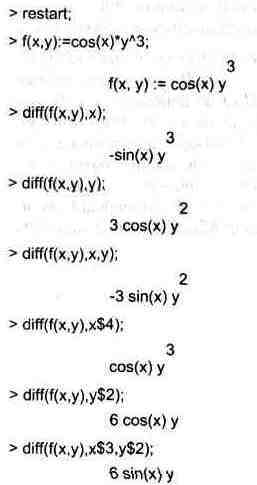
10.3.2. Дифференциальный оператор D
Для создания функций с производными может также использоваться дифференциальный оператор D. Порою он позволяет создавать более компактные выражения, чем функции diff и Diff. Дифференциальный оператор можно записывать в следующих формах:
D(f) или D[i](f),
где: параметр f — выражение или имя функции, i — положительное целое число, выражение или последовательность. Оператор D(0 просто вычисляет имя производной от f, поскольку в этой форме он эквивалентен unapply(diff(f(x),x),x). В форме D(f)(x) этот оператор подобен diff(f(x),x).
Приведем примеры на дифференцирование функций заданных только именами и функций с одним параметром:
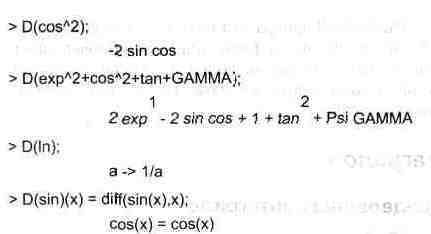
Следующий пример показывает дифференцирование функции пользователя fun с применением дифференциального оператора D и функции din:
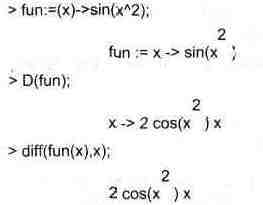
Дифференциальный оператор можно применять и для дифференцирования функций ряда переменных по заданной переменной:
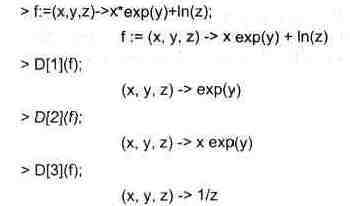
Пример применения дифференциального оператора для функции f, заданной программным объектом — процедурой, представлен ниже:
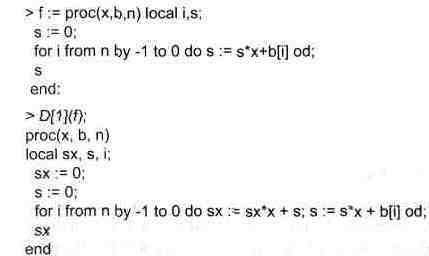
Этот пример показывает реализацию схемы Горнера для полинома b степени п от переменной х. При этом применение оператора дифференцирования возвращает процедуру. Ряд интересных возможностей по вычислению производных предоставляет пакет расширения student, описанный в главе 12. В нем, кстати, дифференциальный оператор переопределяется.
10.4. Вычисление интегралов 10.4.1. Вычисление неопределенных интегралов
Вычисление неопределенного интеграла J f(x) dx
обычно заключается в нахождении первообразной функции. Это одна из широко распространенных операций математического анализа.
Для вычисления неопределенных и определенных интегралов Maple V предоставляет следующие функции:
int(f,x) int(f,x=a..b) int(f,x=a..b,continuous) Int(f,x) Int(f,x=a..b) Int(f,x=a..b,continuous)
Здесь: f — подынтегральная функция, х — переменная, по которой выполняются вычисления, а и b — нижний и верхний пределы интегрирования, continuous — опционально заданное условие.
Maple V старается найти аналитическое значение интеграла с заданной подынтегральной функцией. Если это не удается (например, для интегралов в закрытой форме), то возвращается исходная запись интеграла. Для вычисления определенного интеграла надо использовать функцию evalf(int(f,x=a..b) ). Ниже приведены примеры вычисления интегралов:
> int(sin(x)/x,x);
S'li-K)
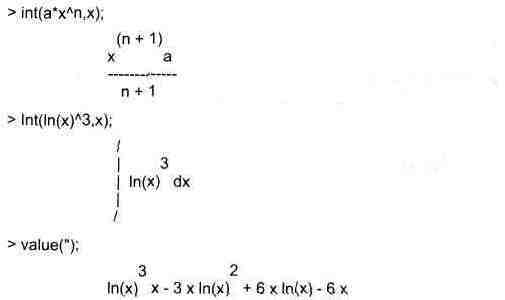
Обратите внимание, что в аналитическом представлении неопределенных интегралов отсутствует произвольная постоянная С. Не следует забывать о ее сущест-вонапии. Для вычисления кратных интегралов (двойных, тройных и т.д.) следует
Вычисление интегралов 175
применять функцию int (или Int) внутри такой же функции, делая это столько раз, сколько нужно — например, два или три раза при вычислении двойных или тройных интегралов. В отличие от функции дифференцирования для функции интегрирования нельзя задавать подынтегральные функции в виде списка или множества.
Возможно вычисление сумм интегралов и интегралов сумм, а также интегралов от полиномов.
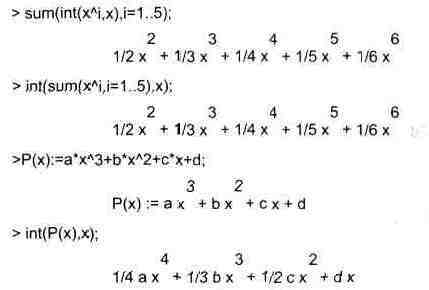
В некоторых случаях Maple V не может вычислить интеграл. Тогда она просто повторяет его. С помощью функций taylor и convert можно попытаться получить аналитическое решение в виде полинома, что демонстрирует следующий характерный пример:
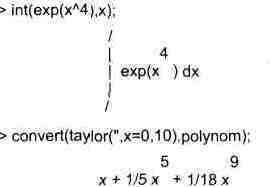
Более подробно об этих операциях говорится в разделе 10.6.1. Разумеется, существует и множество иных возможностей и приемов для выполнения операции интегрирования. В дальнейшем мы неоднократно будем рассматривать и другие, более специфические функции для осуществления интегрирования и вычисления интегральных преобразований. В частности, ряд средств вычисления интегралов реализован в пакете расширения student, описанном в главе 12.
10.4.2. Вычисление определенных интегралов
Другой важной операцией является нахождение в аналитической или численной форме определенного интеграла
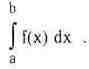
176 Операции и функции математического анализа
Для вычисления определенных интегралов используются те же функции int и Int, в которых надоно указать пределы интегрирования, например, х=а..Ь, если интегрируется функция переменной х. Это поясняется приведенными ниже примерами:

Как видно из этих примеров, значениями пределов может быть бесконечность, обозначаемая как unfinity.
Наличие у функции особых (сингулярных) точек нередко затрудняет выполнение с ней ряда операций, например, численного интегрирования. В этом случае могут помочь соответствующие опции:

10.4.3. Вычисление кратных интегралов
Функции int и Int могут использоваться для вычисления кратных интегралов. Для этого они используются неоднократно.
На рис. 10.1 представлено вычисление тройного интеграла последовательным троекратным применением функции интегрирования. При этом входное выражение представлено в естественной математической форме, что для данной операции (интегрирования) выглядит более наглядно, чем запись функций int трижды с вложениями.
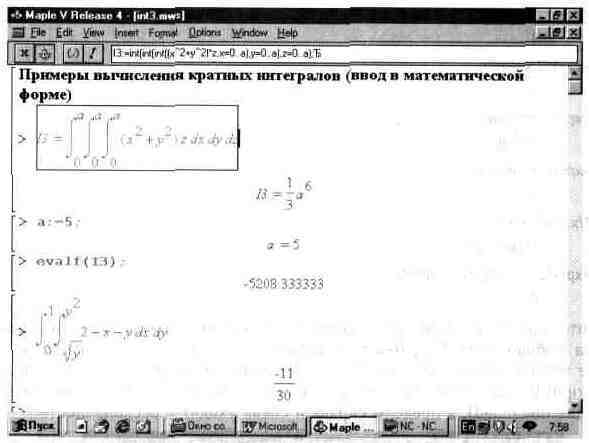
Рис. 10.1. Вычисление кратных интегралов.
Как видно из второго примера на рис. 10.1, возможно вычисление интегралов, у которых пределы являются функциями.
В пакете расширения student имеются дополнительные функции интегрирования, которые дополняют уже описанные возможности.
10.5. Вычисление пределов функций
Для вычисления пределов функции f в точке х=а используются следующие функции:
limit(f,x=a) limit(f,x=a,dir) Limit(f,x=a) Limit(f,x=a,dir)
Здесь: f — алгебраическое выражений, х — имя переменной, dir — опция, указывающая на направление поиска предела (left — слева, right — справа, real — в области вещественных значений, complex — в области комплексных значений). Значением а может быть бесконечность (как положительная, так и отрицательная). Примеры применения этих функций приведены ниже:
> Limit(sin(x)/x,x=0);
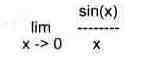
> value("):
> Limit(1-exp(-x),x=infinity);
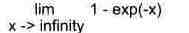
> value(");
1 >'limit(s^n(x)л2,x=Pi/2);
, 1 > (imit(exp(x), x=infinity);
> infinity i' > fimit(exp(x), x=-infinity);
0 > limit(1/x, x=0, real);
undefined > lim^t(exp(xл2)«(1-erf(x)), x=infinity);
0
Обратите внимание на то, что в первом примере фактически дано определение предела в общем виде. Рис. 10.2 показывает вычисление пределов функции tan(x) в точке х=л/2, слева и справа от нее. Для указания направления используются опции right (справа) и left (слева). Видно, что в самой точке предел не определен (значение undefined), а пределы справа и слева уходят в бесконечность.
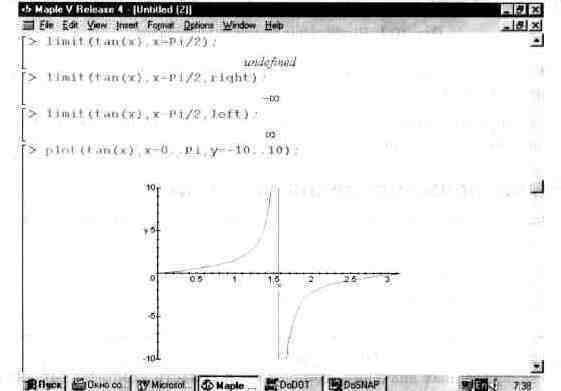
Риг. 10.2. Пример вычисления пределов функции tan(x) и построение ее графика.
Показанный на рис. 10.2 график функции tan(x) наглядно подтверждает существование бесконечных пределов справа и слева от точки х=я/2 и отсутствия его в самой этой точке, где функция испытывает разрыв от значения +°° до -°°.
10.6. Разложение функций в ряд 10.6.1. Разложение в степенной ряд
Для разложения функции или выражения ехрг в ряд служат следующие основные функции:
series(expr, eqn) и series(expr, eqn, n)
Здесь: ехрг — разлагаемое выражение, eqn — условие (например, в виде х = а) или имя переменной (например, х) и n — необязательное и неотрицательное целое число, задающее число членов ряда (при отсутствии его оно по умолчанию берется равным 6, но может переустанавливаться системной переменной Order). Если в качестве eqn задано имя переменной, это соответствует разложению по этой переменной в области точки с ее нулевым значением. Задав eqn в виде х^хО, можно получить разложение по переменной х в окрестности точки х=х0.
Разложение получается в форме степенного многочлена. Остаточная погрешность задается членом вида 0(х"). При точном разложении этот член отсутствует. В общем случае для его удаления можно использовать функцию convert.
Ниже представлены примеры разложения различных выражений в ряд:
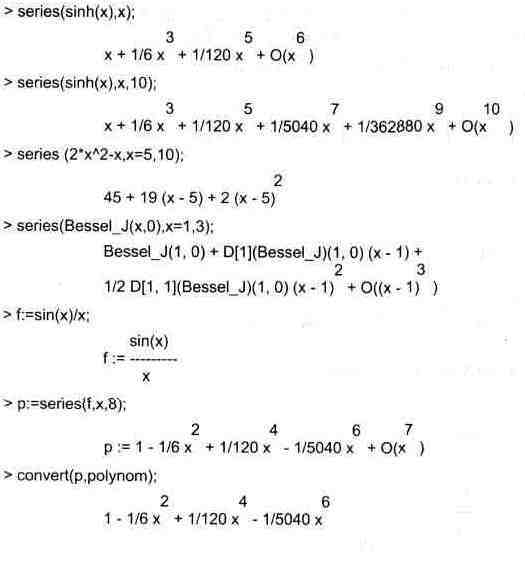
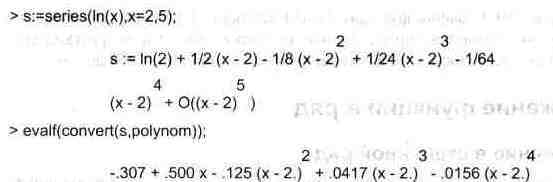
Здесь видно, что член, дающий ошибку, отсутствует в тех разложениях, которые точны — например, в разложениях степенных многочленов. Для визуализации точности приближения рядами заданных аналитических зависимостей очень полезно построить на одном графике кривые аналитической зависимости и разложения в ряд. Мы это покажем чуть позже на примере ряда Тейлора.
10.6.2. Разложение в ряды Тейлора и Маклорена
Для разложения в широко распространенный ряд Тейлора используется функция:
taylor(expr, eq/nm, n)
Здесь: expr — разлагаемое в ряд выражение, eq/nm — равенство (в виде х = а) или имя переменной (например х), n — необязательный параметр, указывающий на порядок разложения и представленный целым положительным числом (при отсутствии указания порядка он принимается по умолчанию равным 6). При задании eq/nm в виде х=а разложение готовится относительно точки с х=а. При указании eq/nm в виде просто имени переменной разложение ищется в окрестности нулевой точки, т.е. фактически вычисляется ряд Маклорена.
Ниже представлены примеры применения функции taylor:
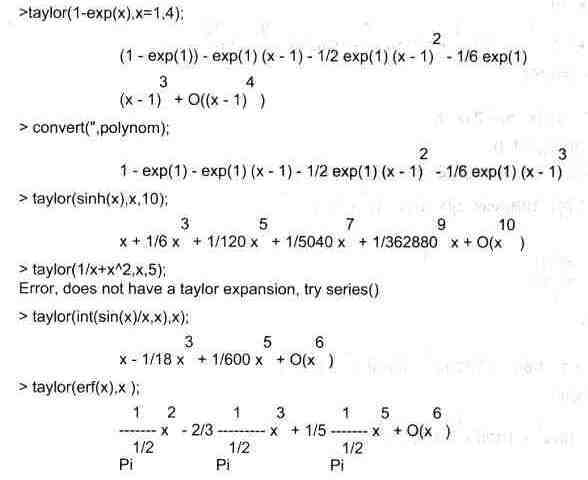
Разложение функций в ряд
181
На рис. 10.3 дан пример разложения в ряд Тейлора функции sin(x) с построением ее графика и графика по разложению в ряд. Это хороший пример визуализации результатов математических вычислений; отлично видно, что при малых х график ряда практически повторяет разлагаемую функцию, но затем начинает сильно от нее отходить. Можно буквально в считанные секунды попробовать изменить число членов ряда или диапазон изменения переменной х. При этом легко убедиться в том, что при больших х поведение ряда не имеет ничего близкого к поведению разлагаемой в ряд функции — в частности нет и намека на периодичность разложения, которая присуща тригонометрической функции sin(x).

Рис. 10.3. Разложение в ряд Тейлора функции sin(x) и построение ее графика.
Для разложения в ряд Тейлора функции ряда переменных используется функция:
mtaylor(f, v) или mtaylor(f, v, n) или mtaylor(f, v, n, w).
Здесь: f — алгебраическое условие, v — список имен или равенств, п — необязательное число, задающее порядок разложения; w — необязательный лист целых чисел, задающих «вес» каждой переменных списка v. Эта функция должна вызываться из библиотеки Maple V:
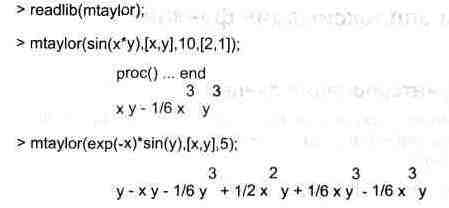
Для получения только коэффициента при члене k-го порядка ряда Тейлора можно использовать функцию coeftayl(expr,var,k). Если expr — функция ряда переменных, то k должен задаваться списком порядков коэффициентов.
10.6.3. Вычисление асимптотических и иных разложений
Для вычисления асимптотических разложений функций (в виде рядов) используются следующие функции:
asympt(f,x) или asympt(f,x,n)
Здесь: f — функция переменной х или алгебраическое выражение, х — имя переменной, по которой производится разложение, n — положительное целое число (порядок разложения, по умолчанию равный 6). Рис. 10.4 показывает примеры применения этой функции.

Рис. 10.4. Применение функции asympt.
Помимо указанных выше Maple V имеет множество функций для иных разложений выражений в ряд. Например, в пакете расширения numapprox (см. главу 12) имеется функция laurent(expr,var,n), позволяющая получить разложение в ряд Лорана, функция chebyshev(expr, eq/nm, eps) дает разложение в форме полиномов Чебышева и т.д.
10.7. Интерполяция и аппроксимация функций и данных
10.7.1. Полиномиальная интерполяция данных
Если данные некоторой зависимости у(х) заданы векторами Х и Y ее дискретных значений, то для получения интерполяционного степенного многочлена — полинома можно использовать функцию:
interp(X,Y,v ) или в инертной форме Interp(X,Y, v)
Переменная v указывает имя переменной интерполяционного полинома. Векторы Х и Y должны содержать п+1 координат точек исходной зависимости, где n — степень интерполяционного полинома.
Рис. 10.5 показывает технику применения полиномиальной аппроксимации на основе функции interp с построением графика исходных точек и аппроксимирующего полинома. Нетрудно заметить, что график полинома проходит точно через исходные точки — они даны квадратиками.
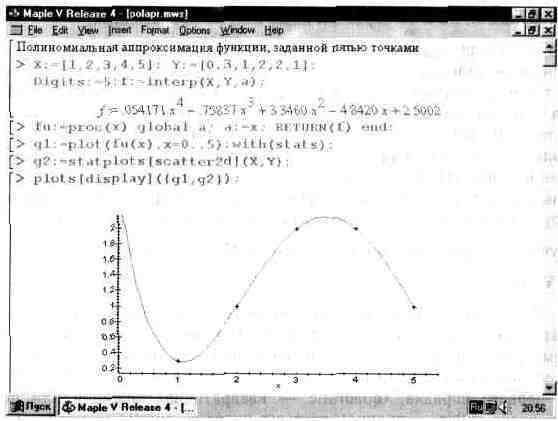
Рис. 10.5. Пример осуществления полиномиальной аппроксимации.
В этом примере полезно присмотреться к визуализации результатов вычислении и построению совместно графика интерполяционного полинома и исходных точек. В частности, для построения последних использованы средства пакета stats, позволяющие выводить на график точки с заданными координатами, причем не только в виде точек, но и в виде маленьких крестиков, кружков, квадратов и других фигур. Для выбора типа точек и других параметров графика его надо выделить (установив курсор мыши в поле графика и щелкнув левой клавишей мыши) и нажать правую клавишу мыши — появится контекстно-зависимое меню с операциями форматирования графика.
Приведем еще несколько примеров использования функции Interp:

10.7.2. Сплайн-интерполяция и аппроксимация
Точность полиномиальной аппроксимации катастрофически падает при увеличении степени аппроксимирующих полиномов. От этого можно избавиться, используя для аппроксимации отрезки полиномов невысокой степени, применяемые для представления части узловых точек. Самым известным методом такой аппроксимации является сплайн-аппроксимация на основе применения отрезков кубических полиномов. При этом аппарат сплайн-аппроксимации позволяет получить полиномы, которые дают непрерывность в узловых точках не только представляемой ими функции, но и ее первых и даже вторых производных.
Наглядно сплайн-функцию можно представить в виде гибкой стальной линейки, закрепленной в узловых точках и плавно изгибающейся. На это указывает и перевод термина «spline» — гибкая линейка. Благодаря указанным свойствам сплайнов они неплохо описывают функции, представленные небольшим числом узловых точек (благодаря плавности сплайн-кривых), и функции, представляемые очень большим числом узловых точек (поскольку порядок полиномов от этого числа уже не зависит). Недостатком сплайн-аппроксимации является отсутствие общего выражения для всей кривой. Фактически приходится использовать набор сплайн-функций для различных интервалов между узловыми точками.
Для получения сплайн-функции используется Maple-функция spline(X,Y,var,d)
где Х и Y — одномерные векторы одинакового размера, несущие значения координат узловых точек исходной функции (причем в произвольном порядке), var — имя переменной, относительно которой вычисляется сплайн-функция и необязательный параметр d задает вид сплайна (linear — линейная функция или полином первого порядка, (quadratic — квадратичная функция или полином второго порядка, cubic — полином третьего порядка, quartic — полином четвертого порядка). Если параметр d опущен, то сплайн-функция будет строиться на основе полиномов третьего порядка (кубические сплайны).
Технику сплайновой аппроксимации наглядно поясняет рис. 10.6. На нем представлено задание векторов Х и Y узловых точек и четырех сплайновых функций, по которым построены их графики. Для одной из функций (с линейной интерполяцией между узлами) показан вид сплайновой функции.
Как видно из рис. 10.6, сплайновая функция представляет собой кусочную функцию, определяемую на каждом отдельном интервале. При этом на каждом участке такая функция описывается отдельным полиномом соответствующей степени. Функция построения графиков plot «понимает» такие функции и позволяет без преобразования типов данных строить сплайновые функции. Для работы с кусочными функциями можно использовать функции convert и piecewise.
10.8. Решение нелинейных уравнений и неравенств
10.8.1. Основная функция solve
Для решения линейных и нелинейных уравнений в аналитическом виде используется достаточно универсальная и гибкая функция
solve(eqn, var) или solve({eqnl,eqn2,...},{varl,var2,...})
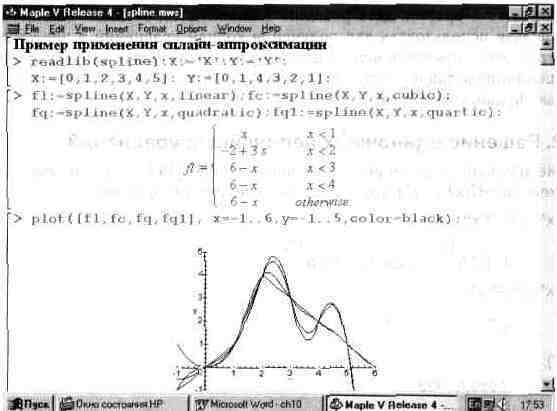
Рис. 10.6. Задание сплайновои аппроксимации и построение графиков полученных функций.
где: eqn — уравнение, содержащее функцию ряда переменных, var — переменная, по которой ищется решение. Как уже отмечалось в главе 1, если решение содержит повторяющиеся выражения, Maple V обозначает их как %1, %2 и т.д. и выводит решение с такими переменными.
Характер решении можно изменить с помощью глобальных переменных:
_SolutionsMayBeLost — при значении true дает решение при возврате функцией solve значения NULL;
_MaxSols — задает максимальное число решении;
_EnvAllSolutions — при значении true задает выдачу всех решений.
В решениях помимо переменных %N могут встречаться следующие обозначения:
_NN — указывает на неотрицательные решения;
_В — указывает на решения в бинарной форме;
_Z — указывает на то, что решение содержит целые числа.
В форме
solve[subtopic]
возможны расширения функции solve следующих типов:
Hoats [unctions identity ineqs linear radical scalar series system
При решении систем уравнений они и список переменных задаются как множества, т.е. в фигурных скобках. При этом и результат решения получается в виде множества. Чтобы преобразовать его к обычному решению, нужно использовать функцию assign, которая обеспечивает присваивание переменным значений, взятых из множества.
Функция solve старается дать решение в аналитическом виде. Это не означает. что ее нельзя использовать для получения корней уравнений в численном виде. Просто для этого придется использовать функцию evalf или convert. Если результат решения представлен через функцию RootOf, то получить все корни можно с помощью функции allvalues.
10.8.2. Решение одиночных нелинейных уравнений
Решение одиночных нелинейных уравнений виде f(x)=0 легко обеспечивается функцией solve(f(x),x) На это указывают следующие примеры:

Часто бывает удобно представлять уравнение и его решение в виде отдельных объектов, отождествленных с определенной переменной:
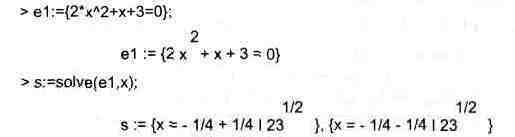
В частности, это позволяет легко проверить решение (даже если оно не одно, как в приведенном примере) подстановкой subs:
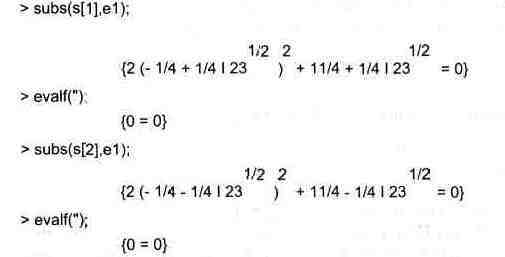
Сводящиеся к одному уравнения вида fl(x)=f2(x) также решаются функцией -olve(fl(x)=f2(x),x):

Обратите внимание в этих примерах на эффективность применения функции ativalues, позволяющей получить решения, выраженные через функцию RootOf в явном виде.
10.8.3. Решение тригонометрических уравнений
Функция solve может использоваться для решения тригонометрических уравнений:

Однако из приведенных примеров видно, что при этом найдено одно главное решение. Периодичность тригонометрических функций и связанная с этим множественность решений при этом проигнорированы. Однако можно попытаться найти все периодические решения, выполнив следующую команду:
> ^EnvAIISolutions:=true;
Указанная в ней системная переменная отвечает за поиск всех периодических решений, когда ее значение равно true, и дает поиск только главных решений при значении false, принятом по умолчанию. Так что теперь можно получить:
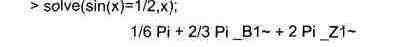
На рис. 10.7 показан более сложный случай решения нелинейного уравнения вида fl(x)=f2(x), где fl(x)=sin(x) и f2(x)=cos(x)-l.
Решение дано в графическом виде и в аналитическом для двух случаев — нахождения главных значений корней и нахождения всех корней.
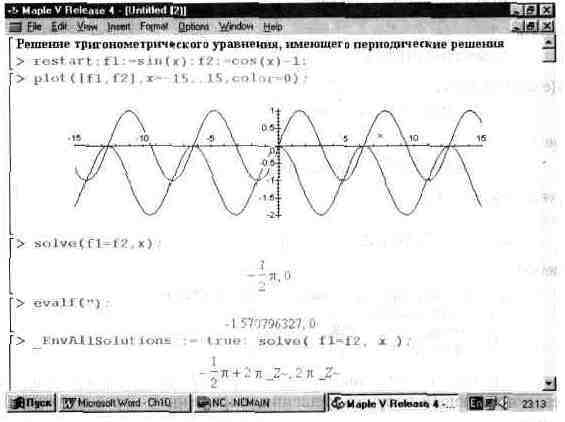
Рис. 10.7. Пример решения уравнения, имеющего периодические решения.
В решениях встречаются переменные _В1~ и _Z1", означающие ряд натуральных чисел. Благодаря этому через них можно представить периодически повторяющиеся решения.
10.8.4. Решение систем нелинейных и трансцендентных уравнений
Функция solve может использоваться для решения систем нелинейных и трансцендентных уравнений. Для этого система уравнений и перечень неизвестных задаются в виде множеств. Ниже приведены примеры решения уравнений:

> unassign('x');y:='y';
y:=y > х;у;
X
У
В этих примерах достаточно отчетливо видна техника работы с функциями solve и assign. В конце примеров показано восстановление неопределенного статуса переменных х и у с помощью функции unassign и снятия определения переменных с помощью заключения их в прямые апострофы.
10.8.5. Функция RootOf
В решениях уравнении нередко появляется функция RootOf, означающая, что корни нельзя выразить в радикалах. Эта функция применяется и самостоятельно в виде:
RootOf(expr) Root0f(expr, x),
где expr — алгебраическое выражение или равенство, имя переменной, относительно которого ищется решение. Если х не указана, ищется универсальное решение по переменной _Z. Когда expr задано не в виде равенства, решается уравнение expr = 0. Для получения решений вида RootOf в явном виде может использоваться функция allvalues.
Примеры применения функции RootOf:

Итак, функция RootOf является эффективным способом представления решения в компактном виде. Как уже отмечалось, наряду с самостоятельным применением она часто встречается в составе результатов решения нелинейных уравнений.
10.8.6. Решение неравенств
Решение неравенств существенно расширяет возможности функции solve. При этом неравенства задаются также, как и равенства.
Приведенные ниже примеры поясняют технику решения неравенств:

В последнем примере показано решение системы неравенств.
10.8.7. Решение функциональных уравнений
Решение функционального уравнения, содержащего некоторую функцию f(x) в составе равенства, заключается в нахождении этой функции. Для этого можно использовать функцию solve, что демонстрируют приведенные ниже примеры:


10.8.8. Решение в численном виде — функция fsolve
Для получения численного решения нелинейного уравнения или системы нелинейных уравнений удобно использовать функцию ;
fsolve( eqns, vars, options ) Эта функция может использовать следующие опции:
complex — находит один или все корни полинома в комплексной форме;
fulldigits — задает вычисления для полного числа цифр, заданного
функцией Digits;
maxsols=n — задает нахождение только п корней;
interval — задается в виде а..Ь или х = а..Ь или {x=a..b, y=c..d, ...}
и обеспечивает поиск корней в указанном интервале.
Функция fsolve дает решения сразу в форме вещественных или комплексных чисел, что и показывают следующие примеры:
> fsolve(sin(x)=0.5);
2.617993878 > fsolve(sin(x)=0.5,x=4..8);
6.806784083 >fsolve(2*xл2+x-1=10,x);
-2.608495283, 2.108495283 > fsolve(x"5-x,x);
0.-1..1. > fsolve(xл5-x,x,complex);
О, -1..-1. I, 1. I, 1.
Заметим, что локализация поиска корней в заданном интервале позволяет отыскивать такие решения, которые не удается получить с помощью функций solve и fsolve в обычном применении.
10.8.9. Решение рекуррентных и иных видов уравнений
Функция solve имеет ряд производных от нее функций. Одну из таких функций fsolve мы рассмотрели выше. В справочной системе Maple V можно найти и ряд других функций, например, rsolve для решения рекуррентных уравнений, isolve для решения целочисленных уравнений, msolve для решения по модулю m и т.д. Здесь мы рассмотрим решение важного класса уравнений — рекуррентных. Напомним, что это такие уравнения, у которых заданный шаг решения находится по одному или нескольким предшествующим шагам.
Для решения рекуррентных уравнений используется (Ьункция rsolve:


Ввиду очевидности примеров воздержимся от более подробного обсуждения этих функции.
Функции solve и fsolve могут решать уравнения, содержащие интегралы и специальные математические (ЬУНКЦИИ:

Обратите внимание на два последних примера — решение уравнения erf(x)=0.5. Функция solve в этом случае находит нетривиальное приближенное решение в комплексной форме, тогда как функция fsolve находит обычное точное решение.
10.9. Решение дифференциальных уравнений
Важное место в математических расчетах занимает решение дифференциальных уравнений. К нему, в частности, обычно относится анализ поведения различных систем во времени (анализ динамики), а также вычисление различных полей. Maple V позволяет решать как одиночные дифференциальные уравнения, так и системы дифференциальных уравнений как аналитически, так и в численном виде.
10.9.1. Решение системы простых дифференциальных уравнений
Для решения системы простых дифференциальных уравнений (задача Коши) используется следующая функция:
dsolve(deqns, vars) или dsolve(deqns, vars, option)
Здесь: deqns — одно дифференциальное уравнение или система из систем дифференциальных уравнений первого порядка с указанием начальных условий, vars — переменная или переменные, относительно которых ищется решение, option — необязательный параметр, указывающий на метод решения.
Параметр option задает один из методов решения:
exact — аналитическое решение (принято по умолчанию);
explicit — решение в явном виде;
laplace — решение через преобразование Лапласа;
series — решение в виде ряда с порядком, указываемым значением переменной Order;
numeric — решение в численном виде.
Для решения задачи Коши в deqns надо включать начальные условия, а при решении краевых задач — краевые условия. Если Maple способна найти решение при числе начальных или краевых условии меньше порядка системы, то в решении будут появляться неопределенные константы вида _С1, _С2 и т.д. Они же могут быть при аналитическом решении системы, когда начальные условия не заданы. Если решение найдено в неявном виде, то в нем появится параметр _Т.
Производные при записи дифференциальных уравнений могут задаваться функцией diff или оператором D. Выражение deqns должно иметь структуру множества и содержать помимо самой системы уравнений их начальные условия.
На рис. 10.8 приведены примеры решения простых дифференциальных уравнений первого и второго порядка в аналитическом виде.

Рис. 10.8. Примеры решения дифференциальных уравнений первого и второго порядка.
На рис. 10.9 представлено решение системы из двух дифференциальных уравнений различными методами — в явном виде, в виде разложения в ряд и с использованием преобразования Лапласа. Здесь следует отметить, что решение в виде ряда является приближенным решением и полученные при этом аналитические выражения отличаются от явного решения и решения с применением преобразования Лапласа.
Следует отметить, что несмотря на обширные возможности Maple V в аналитическом решении дифференциальных уравнений оно возможно далеко не всегда. Поэтому, если не удается получить такое решение, полезно попытаться найти решение в численном виде.
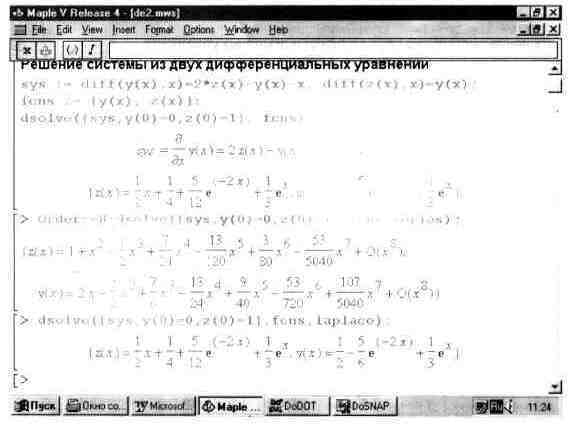
Рис. 10.9. Решение системы из двух дифференциальных уравнении различными методами.
10.9.2. Численное решение дифференциальных уравнений
Для решения дифференциальных уравнений в численном виде используется функция dsolve с опцией numeric или type=numeric. При этом решение возвращается в виде специальной процедуры, по умолчанию реализующей широко известный метод решения дифференциальных уравнений Рунге-Кутта-Фельберга порядка 4 и 5 (в зависимости от условий адаптации решения к скорости его изменения). Эта процедура называется rkf45 и символически выводится (без тела) при попытке решения заданной системы дифференциальных уравнений. Последнее достаточно наглядно иллюстрирует рис. 10.10.
Указанная процедура возвращает особый тип данных, позволяющих найти решение в любой точке или построить график решения (или решений). Для этого Maple предлагает ряд возможностей, и одна из них представлена на рис. 10.12 (см. последнюю строку ввода). При этом используется функция plot[odeplot] из пакета odeplot, предназначенного для визуализации решений дифференциальных уравнений.
Еще один пример решения системы дифференциальных уравнений показан на рис. 10.11. На этот раз на одном графике даны зависимости у(х) и z(x), представляющих полное решение заданной системы. При этом процедура имеет особый вид listprocedure и для преобразования листа выходных данных в векторы решения Y и Z используется функция subs.
В список параметров функции dsolve можно явным образом включить указание на метод решения, например, опция method=dverk78 задает решение методом Рунге-Кутта порядка 7 или 8. С помощью опции 'abserr'=aerr можно задать величину абсолютной погрешности решения, а с помощью опции 'minerr'=mine — минималь-
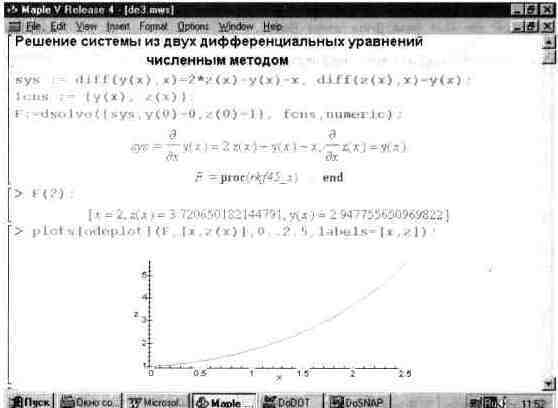
Рис. 10.10. Решение системы дифференциальных уравнении численным методом rkf45 с выводом графика решения.
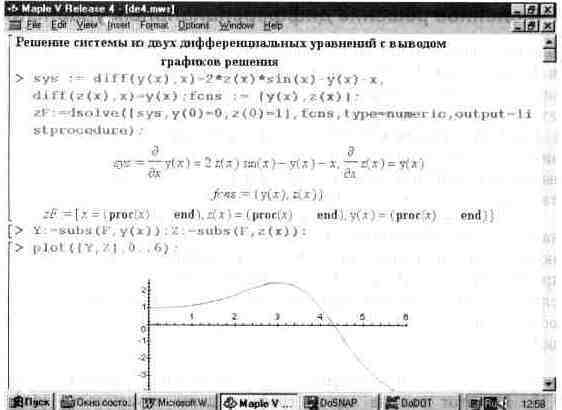
Рис. 10.11. Решение системы дифференциальных уравнений численным методом с выводом всех графиков искомых зависимостей.
ную величину погрешности. В большинстве случае эти величины, заданные по умолчанию, оказываются приемлемыми для большинства расчетов.
Для решения достаточно сложных задач полезны специальная структура DESol для решения дифференциальных уравнений и инструментальный пакет Detools,
содержащий самые изысканные средства для графической визуализации результатов решения дифференциальных уравнений. Эти средства более подробно мы рассмотрим в дальнейшем.
10.9.3. Структура неявного представления
дифференциальных уравнений DESol
В ряде случаев иметь явное представление дифференциальных уравнений не целесообразно. Для неявного их представления в Maple V введена специальная структура
DESol(expr,vars),
где: exprs — выражение для исходной систем дифференциальных уравнений, vars — заданный в виде опции список переменных (или одна переменная).
Структура DESol образует некоторый объект, дающий представление о дифференциальных уравнениях, чем-то напоминающее RootOf. С этим объектом можно обращаться как с функцией, т.е. его можно интегрировать, дифференцировать, получать разложение в ряд и вычислять численными методами. На рис. 10.12 показаны примеры применения структуры DESol.
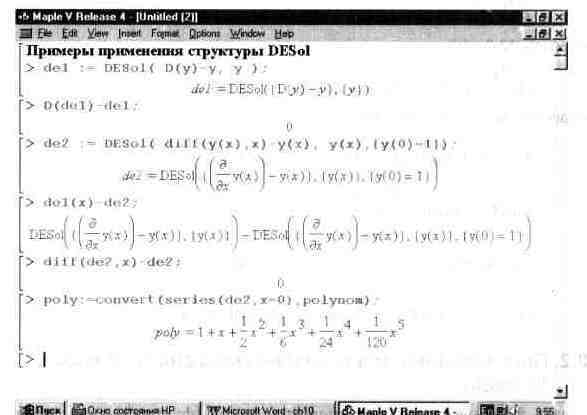
Рис. 10.12. Примеры применения структуры DESol.
Обратите внимание на последний пример. В нем структура DESol использована для получения решения дифференциального уравнения в виде степенного ряда.
10.10. Исследование аналитических функций
Исследование функций обычно заключается в определении координат особых точек функции и ее значений в этих точках. К сожалению, пока нет средств, автоматизирующих исследование аналитических функций и разом дающих все ее характеристики — экстремумы (максимумы и минимумы), корни (дающие нуле-
вые значения функции), точки перегибов и разрывов, асимптоты и т.д. Поэтому функции приходится отдельно анализировать.
С помощью функции solve легко находятся значения независимой переменной х функции вида f(x), при f(x)=0. Ряд функций служит для вычисления экстремумов, максимумов и минимумов функций, а также для определения ее непрерывности.
10.10.1. Поиск экстремумов функций
Библиотечная функция extrema(expr, constr, vars.'nv')
позволяет найти экстремум выражения ехрг при ограничениях constr при переменных var, по которым ищется экстремум. Наиденные координаты точек экстремума присваиваются переменной 'nv'. Эта функция находится в стандартной библиотеке и потому должна вызываться командой readlib(extrema). Параметры vars и 'nv' задаются как опции, т.е. могут и отсутствовать.
Ниже даны поимеоы поименения (ЬУНКЦИИ extrema:

10.10.2. Поиск минимумов и максимумов аналитических функций
Для поиска минимумов и максимумов выражений (функций) ехрг служат функции стандартной библиотеки:
minimize(expr) maximize(expr) minimizefexpr, vars) maxirnize(expr, vars) minimize(expr, vars, 'infinite') maximize(expr, vars. 'infinite') minimize(expr, vars, ranges) maximize(expr, vars, ranges)
Эти функции могут разыскивать максимумы и минимумы как функции одной, так и ряда переменных; они указываются списком переменных vars. Опция 'infinity' означает, что поиск минимума или максимума выполняется по всей числовой оси. а опция r.iii^os позволяет задавать пределы изменения переменных при поиске.
Исследование аналитических функций 199
Примеры применения этих функций, приведенные ниже, наглядно поясняют технику поиска минимумов и максимумов:
> readlib(minimize):
> minimize(-sin(x)/x);
-1
> minimizetx'expt-x), 'infinite');
x exp(-x) > rninirr\ize{x"2 + y"2, {x, y}, {x=-10..10, y=5..20});
25 > readlib(maximize):
> maximize(sin(x)/x);
1 > maximize(x*exp(-x));
exp(-1) > maximize(x"2 + y^, {x, y}, {x=-10..10, y=-10..10});
0
10.10.3. Анализ функций на непрерывность
Функции
iscont(expr, x = а .. b) iscont(expr, x = а .. b, 'closed')
позволяют исследовать выражение ехрг в виде зависимости от переменной х на непрерывность. Если выражение непрерывно, возвращается логическое значение true, иначе — false. Опция 'closed' показывает, что конечные точки должны также проверяться.
Другая функция discont(f, х)
позволяет определить точки, в которых нарушается непрерывность функции f(x). Она вычисляет все точки в пределах изменения х от -°° до +°°. Результаты вычислений могут содержать особые экстра-переменные с именами вида _Zn~ и _NNn"". В частности, они позволяют оценить периодические нарушения непрерывности функций.
Примеры применения функции iscont и discont приведены ниже:
> readlib(iscont):
> iscont( 1/х, х=0..1 );
true > iscont( 1/х, х=0..1,'closed');
false > iscont( tan(x), x=O..Pi/2 );
true
200 Операции и функции математического анализа
> iscont( tan(x), x=O..Pi/2, 'closed');
false > iscont( 1/(x+a), x=-1..1);
FAIL >discont(arctan(1/2•tan(2»x))/(xл2-1),x);
{-1,1, 1/2 Pi_Z4~+ 1/4 Pi} >discont(1/(x-2),x);
{2} >discont(1/((x-1)*(x+2)),x);
{1.-2} > discont(sin(x)/x,x);
{0} > discont(GAMMA(x/2),x);
{-2 _NN5~}
10.10.4. Нахождение сингулярных точек
Многие операции, например интегрирования и дифференцирования, чувствительны к особенностям функций, в частности, к ее разрывам и особым точкам. Функция
singular(expr, vars)
позволяет найти особые (сингулярные) точки выражения ехрг, в которых она испытывает разрывы. Список переменных может указываться опционально.
Примеры применения этой функции приведены ниже:
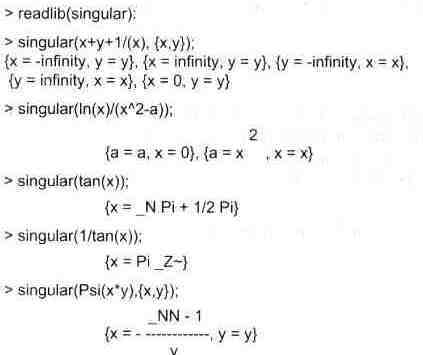
Появление и трактовка специальных переменных в результатах вычислений этой функции уже пояснялась ранее. Комбинированное применение всех описанных в этом разделе функций позволяет получить достаточно полные и точные данные об исследуемых функциях.
10.11. Функции из отдельных кусков — piecewise
Для создания функций, составленных из отдельных кусков, Maple V располагает интересной функцией
piecewise(cond_l,f_l, cond_2,f_2, .... cond_n,f_n, f_otherwise),
где: f_i — выражение, cond_i — логическое выражение, f_otherwise — определяемые опционально выражения. В зависимости от того или иного условия эта функция позволяет формировать ту или иную аналитическую зависимость.
Рис. 10.13 показывает задание функции f(x), содержащей три характерных участка. По определенной через функцию пользователя зависимости f(x) можно, как обычно, построить ее график.

Рис. 10.13. Пример задания и применения функции, составленной из отдельных кусков.
Важно отметить, что созданная с помощью piecewise зависимость может участвовать в различных преобразованиях. Например, на рис. 10.13 показано, что она дифференцируется и можно построить график производной этой функции. При этом каждая часть функции обрабатывается отдельно.
10.12. Прямое и обратное Z-преобразования
Прямое и обратное Z-преобразования широко используются в решении задач автоматического управления. Эти преобразования задаются функциями:
ztrans(f, n, z) — прямое преобразование функции f(n) в f(z);
invztrans( f, z, n) — обратное преобразование f(z) в i(n).
Заметим, что прямое Z-преобразование базируется на соотношении ztrans(f(n),n,z) = &ит(^(п)/г'п.п=0.. infinity), представленном на Maple-языке. Примеры применения Z-преобразований представлены ниже:

Z-преобразования осуществляются функциями ядра и стандартной библиотеки. В главе 12 будет рассмотрен ряд других интегральных преобразований, в частности, Лапласа и Фурье, которые реализуются с помощью пакета расширения inttrans (интегральные преобразования).