10.htm

Глава 9. Основные понятия входного языка системы Maple V

9.1. Выражения и основы работы с ними 9.1.1. Алфавит Maple-языка и его синтаксис

Maple-язык является входным языком общения с системой Maple V и одновременно языком ее программирования. Входящие в него средства (прежде всего операторы и функции) подобраны настолько полно и удачно, что при решении подавляющего большинства типовых математических задач от пользователя не требуется знаний даже основ программирования. Достаточно составить алгоритм решения нужной задачи и подобрать набор нужных для его реализации функций и иных средств Maple-языка.

В тоже время Maple-язык один из самых мощных языков программирования математических задач, намного превосходящий по своим возможностям такие известные языки программирования, как Fortran, Algol, PL, Basic, Pascal и др. Это связано прежде всего с возможностью использования в его программных модулях почти 2500 (в реализации R5 2700) операторов, команд и функций, входящих в ядро, основную библиотеку (см. Приложение 1) и в пакеты расширений (см. главу 12) системы Maple V. В тоже время относящаяся к традиционному программированию часть Maple-языка реализована с помощью довольно скромного набора специальных знаков и зарезервированных слов.

Maple-язык является как бы саморасширяющимся и легко адаптируемым к решению конкретных задач любого пользователя. Свыше 90% всех определении системы Maple V, в частности все пакеты расширений и огромная SHARE-библи-отека пользователей, написаны на этом языке. Поэтому знание этого языка является определяющим в серьезном изучении системы Maple V. Ниже Maple-язык описывается как типичный язык программирования.

Алфавит Maple-языка содержит 26 малых латинских букв от а до z, 26 больших латинских букв (от А до Z), 10 арабских цифр (от 0 до 9) и 32 специальных символа (арифметические операторы +, -, *, /, знак возведения в степень " ) и др. Все они будут рассмотрены в данной главе. Имеется пять пар альтернативных символов:

' и ** [ и (¦ ] и ¦) { и (* } и *)

К специальным одиночным и составным знакам относятся элементы синтаксиса языка:

Фиксатор выражения, предотвращающий вывод результата вычисления в ячейку вывода.

,

Фиксатор выражения, дающий вывод результата вычисления в ячейку вывода.

#

Указатель программного комментария.

•

Ограничитель строки (например, 'string').

Выражения и основы работы с ними 101

:=»

Оператор присваивания (например, х:=5).

,,

Пустой оператор.

Указатель типа переменной (например, n::integer или z::complex).

Комментарии в программе, не выводимые в ячейки вывода, задаются после символа #. В них допустимо использовать всё символы кодовых таблиц, что важно при вводе русскоязычных комментариев, использующих символы кириллицы. Применение последних для идентификаторов (имен) объектов недопустимо.

Зарезервированные слова используются для создания условных выражении, циклов, процедур и управляющих команд. Список зарезервированных слов дан ниже.

Зарезервированные слова языка программирования

! # ERROR assignment break by do done elif else empty fi for from function if in next od proc quit read restart save separator stop then while

К зарезервированным относятся также слова, используемые при работе с множествами (intersect, minus, union), логические операторы (and, not и or) и оператор модуля mod. Зарезервированные слова имеют особый статус. Их нельзя использовать в качестве идентификаторов для переменных, функций, процедур и т.д.

Совокупность правил, по которым записываются определения всех объектов Maple-языка, называются его синтаксисом. Некоторые особенности синтаксиса полезно знать сразу, в начале освоения системы. Например, то, что знак - (минус) имеет двойное значение. Применительно к одному числу, переменной или выражению он меняет их знак. Однако два знака минус подряд (например, в записи - -3) задавать нельзя. Другое назначение знака минус — создание операции вычитания, например, 5-2 или а-Ь. Соответственно двойное назначение имеет и знак +, причем число без знака считается положительным, так что +5=5.

При вводе действительных чисел с порядком для ввода порядка используется символ е (например 10е100 или Юе-100). Для изменения общепринятого приоритета вычислений используются круглые скобки, в них же задаются параметры функций и процедур. Более подробно синтаксис Maple-языка рассматривается ниже.

Некоторые операторы представлены двумя символами — например оператор, присваивания переменным их значения := содержит двоеточие и знак равенства. В таких операторах между символами недопустим знак пробела. Однако его можно использовать между отдельными частями выражений; так, (а+Ь)/с эквивалентно (а + b) / с.

По набору операторов и функций Maple-язык намного превосходит любой универсальный язык программирования. Это позволяет, наряду с обычными программными конструкциями, задавать множество специальных конструкций, подчас резко упрощающих запись математических выражений. К примеру, возможна работа со списками имен функций. Язык Maple V имеет множество операций над символьными выражениями и гибкий аппарат создания и преобразования типов данных и результатов вычислений.

102 Основные понятия входного языка системы Maple V

Для большинства пользователей возможности языка Maple V кажутся явно избыточными, так как большинство наиболее распространенных операции в нем реализуется несколькими способами. Однако каждый пользователь волен выбирать из множества возможностей именно те, которые ему необходимы в его конкретной предметной области. Поскольку таких областей превеликое множество, обширные возможности Maple V лишними не являются.

9.1.2. Выражения и их ввод

Фактически Maple V — это система для манипулирования с математическими выражениями. Выражение в системе Maple V — это объект, вполне соответствующий сути обычного математического выражения. Оно может содержать операторы, операнды и функции с параметрами. В этой главе выражения записываются на Maple-языке без использования специальных средств по их представлению в естественном математическом виде. Благодаря этому запись выражений и приводимых примеров одинаково пригодна для любой реализации системы Maple V — даже под MS-DOS. Такая запись получается наиболее короткой, ее можно выводить и распечатывать без применения графических средств. Кроме того, она соответствует виду, принятому в справочной системе Maple V.

Однако пользовательский интерфейс системы Maple V R4 под Windows позволяет представлять как вводимые, так и выводимые выражения в самых различных формах, в том числе в естественном математическом виде (примеры этого многократно приводились и будут приведены в дальнейшем). Maple V имеет многочисленные функции преобразования форматов, позволяющие менять форму представления данных. Там, где нужна повышенная наглядность примеров, они будут приводиться в виде копий экрана.

Выражения в Maple могут эволюционировать, т.е. изменяться в соответствии с заданными математическими законами и правилами преобразования. Например, функция упрощения выражений simplify способна упрощать многие математические выражения, записанные в качестве ее параметра (в круглых скобках):

> simplify(sin(x)л2+cos(x)л2);

>s^mplify((aл2-2ta•»Ы-ЬЛ2)/(a-Ь));

а-Ь

Символьные преобразования и вычисления математических выражений более подробно будут рассмотрены в следующей главе.

Для выполнения любых математических операций необходимо обеспечить ввод в систему исходных данных — в общем случае математических выражений. Для ввода таких выражений и текстовых комментариев служат два типа строк ввода — для ввода математических выражений и текстовых комментариев. Переключение типа текущей строки ввода осуществляется клавишей F5. Строка ввода математических выражений имеет отличительный символ >, а строка ввода текстов никаких признаков не имеет.

В строке ввода может быть несколько выражений. Фиксаторами их могут быть символы ; (точка с запятой) и : (двоеточие). Символ ; фиксирует выражение и задает вывод результатов их вычислений. А символ : фиксирует выражения и

Выражения и основы работы с ними 103

блокирует вывод результатов их вычислений. Фиксаторы выполняют также функцию разделителен выражений, если в одной строке их несколько.

Ввод фиксируется нажатием клавиши Enter. При этом маркер ввода (жирная мигающая вертикальная черта) может быть в любой позиции строки. Если надо перенести ввод на новую строку ввода, следует нажимать клавиши Shift и Enter совместно. С помощью от одного до трех знаков " (прямые кавычки) можно вызывать первое, второе или третье выражение с конца сессии:

> 1:2:3:

> ";

> 1:2:3:

> " ";

2 > 1:2:3:

> " " ";

>2+3:

>";

Следует отметить, что в реализации R5 знак ", называемый ditto-оператором, заменен на знак % (процент).

Особая роль при вводе выражении принадлежит знакам прямого апострофа (одиночного ' или двойного "). Заключенное в такие знаки выражение освобождается от одной пары (закрывающего и открывающего знака '):

> "factor(aл2+2*a*b-Ь'\2)";

2 2

'factor(a + 2 a b - b )'

> 'factor(an2+2''a*b-bA2)';

2 2

factor(a + 2 a b - b )

> factor(aл2+2•atb+bл2);

(a+b)

Некоторые другие возможности обрамления выражений апострофами мы рассмотрим позже. Наиболее важная из них — временная отмена выполненного ранее присваивания переменным конкретных значений.

Для завершения работы с текущим документом достаточно исполнить команду quit, done или stop набранную в строке ввода (со знаком ; в конце). При всех закрытых документах экран системы модифицируется — окна документов исчезают, экран приобретает серый фон, а главное меню имеет всего две позиции (File и Help). Позиция File дает доступ к команде открытия нового документа New или к операции загрузки документа Open.

104 Основные понятия входного языка системы Maple V

9.1.3. Оценивание выражений

Встречая выражение, Maple V оценивает его, т.е. устанавливает возможность эволюции выражения. Если выражение — скалярная переменная, то ее значение будет выведено в ячейке вывода. Для переменных более сложных типов выводится не их значение, а просто повторяется имя переменной. Просто повторяются также имена неопределенных переменных.

Для оценивания выражений различного типа существует группа функций, основные из которых перечислены ниже:

eval(array)

Возвращает содержимое массива array.

evalf(expr, n)

Вычисляет ехрг и возвращает вычисленное значение в форме числа с плавающей точкой, имеющего n цифр после десятичной точки.

evalhf(expr)

Вычисляет ехрг и возвращает вычисленное значение с точностью, присущей данной компьютерной системе.

evalf(int(f, x=a..b))

Оценивает и возвращает значение определенного интеграла int(f,x=a..b).

evalf(Int(f, x=a..b))

Оценивает и возвращает значение определенного интеграла, заданного инертной функцией Int(f,x=a..b).

evalf(Int(f, x=a..b. digits, flag))

Аналогично предыдущему, но возвращает значение интеграла с заданным числом цифр после десятичной точки digits и со спецификацией метода вычислений flag.

evalm(mexpr)

Вычисляет значение матричного выражения mexpr и возвращает его.

evalb(bexpr)

Вычисляет и возвращает значения логических условий.

evalc(cexpr)

Вычисляет значение комплексного выражения.

evalr(expr, ampi)

Оценивает и возвращает значения интервальных выражений (функция должна вызываться из библиотеки).

shake(expr, ampi)

Вычисляет интервальное выражение.

Для функции evalf параметр n задается опционально, при его отсутстии полагается п=10, т.е. вещественные числа выводятся с мантиссой, имеющей десять цифр после десятичной точки.

В выражении ехрг могут использоваться константы (например, Pi, exp(l), гамма) и функции (например, exp, In, грех, arctan, cosh, GAMMA и erf). В матричном выражении mexpr для функции evalm могут использоваться операнды в виде матриц и матричные операторы &*, +, - и ". В комплексных выражениях сехрг наряду с комплексными операндами вида (а + I*b) могут использоваться многие математические функции:

sin

cos

tan

csc

sec

cot

sinh

cosh

tanh

csch

sech

coth

arcsin

arccos

arctan

arccsc

arcsec

arccot

arcsinh

arccosh

arctanh

arccsch

arcsech

arccoth

exp

In

sqrt

abs

conjugate

polar

argument

signum

csgn

Re

Im

Ei

LambertW

dilog

surd

Примеры на применение функций оценивания даны ниже:

> evalhf(sin(l)):

.8414709848078965 >evalm(20*A+1);

[21 40]

[ I [60 81]

>1<3;

1 <3 >evalb(1<3);

true > readlib(evalr):

> readlib(shake):

> evalr(min(2,sqrt(3)));

1/2 3

> evalr(abs(x));

[INTERVAL(x, 0 .. infinity), -INTERVAL(x, -infinity .. 0)] > shake(Pi,3);

INTERVAL(3.1102 ..3.1730)

В дальнейшем мы многократно будем применять функции оценивания для демонстрации тех или иных вычислении.

9.1.4. Последовательности выражений

Maple V может работать не только с одиночными выражениями, но и с последовательностями выражений. Последовательность выражении — это ряд выражении, разделенных запятыми и завершенных фиксатором:

> 1,2+3,a-b,sin(1.0);

1,5,a-b, .8414709848

Для автоматического формирования последовательности выражении применим специальный оператор $, после которого можно указывать число выражений или задавать диапазон формирования выражений:

>f$5;

f, f, f, f, f >$1..6;

1,2,3,4, 5,6 >{\"2+'\)У\='\..5\

2,5,10, 17,26 >V[i]$i=1..5;

V[1], V[2], V[3], V[4], V[5]

Для создания последовательностей выражений можно использовать и функцию seq:

> seq(2*sin(x/10.0),x=0..5);

О, .1996668333, .3973386616, .5910404134, .7788366846, .9588510772

106 Основные понятия входного языка системы Maple V

> seq(f(1 ),f=[sin,cos,tan]);

sir>(1),cos(1),tan(1)

> seq(f(1.),f=[sin,cos,tan]);

.8414709848, .5403023059, 1.557407725

9.1.5. Наборы выражений

Любые выражения могут включаться также в' неупорядоченные наборы. Они создаются с помощью фигурных скобок { }:

> {d,a,c,a,a,c,d,e};

{d, а, с, е} > {1+2,3,5,2+3,6};

{3, 5, 6} > {'Hello','my','friend!'};

{friend!, Hello, my}

Отличительная черта наборов — автоматическое устранение из них повторяющихся по значению элементов. Кроме того, Maple может переставлять элементы наборов.

9.1.6. Списки выражений

Для создания упорядоченных наборов-списков служат квадратные скобки [ ]:

> [d,a,c,a,a,c,d,e];

[d, а, с, а, а, с, d, е] > [1+2,3,5,2+3,6];

[3, 3, 5, 5, 6] > ['Hello','my','friend!'];

[Hello, my, friend!]

Как нетрудно заметить, элементы списков преобразуются и выводятся строго в том порядке, в каком они были заданы. Списки широко применяются для задания векторов и матриц. В ряде случаев, например, для подготовки данных для 20-графи-ков, возникает необходимость в подготовке списка парных списков — например, координат точек (х,у) графика. Для этого можно использовать функцию:

zip(f, u, v) или zip(f, u, v, d)

Здесь f — бинарная функция, u,v — списки или векторы и d — опционально заданное значение. Примеры применения функции zip даны ниже:

>Х:=[1,2,3,4,5]:

>Y:±[3,2,1,2.5,3.5]:

> pare:=(X,Y)->[X,Y];

pare := (X, Y) -> [X, Y] > CoordXY:=zip(pare,X,Y,2);

CoordXY := [[1, 3], [2, 2], [3, 1], [4, 2.5], [5, 3.5]] > zip((X,Y)->X+Y,X,Y);

[4, 4, 4, 6.5, 8.5]

Типы данных

107

Описанные выше преобразования выражений составляют небольшую часть возможностей, которые система Maple предоставляет пользователю. Некоторые другие возможности мы рассмотрим в дальнейшем (см., в частности, главу 11), а пока приступим к более систематизированному обзору средств входного языка системы Maple V.

9.1.7. Метки % в выражениях и вывод выражений

При выполнении порой даже простых операций результаты получаются чрезвычайно громоздкими. Для повышения наглядности выражений Maple V выводит их с выделением общих частей выражений и с присвоением им соответствующих меток. Метки представлены символом %N, где N — номер метки.

Помимо меток при выводе результатов вычислений могут появляться и другие специальные объекты вывода, например, корни RootOf, члены вида 0(х"), учитывающие погрешность в разложении функций в ряд и обозначения различных специальных функций, таких, как интегральный синус, гамма-функция и др. Примеры этого показаны на рис. 9.1.

Рис. 9.1. Примеры, в решении которых фигурируют специальные обозначения.

Часто встречаются также знаки ' для отметки предполагаемых переменных, постоянные интегрирования и другие специальные обозначения. Такие объекты вывода будут описаны по мере их появления.

9.2. Типы данных

9.2.1. Числа и числовые константы

Maple V работает с числами следующего типа: целыми десятичными (О, 1, 123, -456 и т.д.), рациональными в виде отношения целых чисел (7/9, -123/127 и т.д.), вещественными с мантиссой и порядком (1.23Е5, 123.4567Е-10) и комплек-

108 Основные понятия входного языка системы Maple V

сными (2+3*1). В качестве разделителя целой и дробной части мантиссы используется десятичная точка, мнимая единица у комплексных чисел обозначается как 1. Функции Re(x) и Im(x) возвращают действительную и мнимую часть комплексных чисел. Примеры чисто численных операций приведены ниже:

> 2+3/4;

11/4

> 2+3*4;

> (2+3)*4;

20 > 1.0/3;

.3333333333 > 1/3;

1/3 >1.234Е10;

11 .1234 10

> x:=2+7*l;

x:=2+7l > Re(x);

2 > lm(x);

Как видно из этих примеров, ввод и вывод чисел имеет следующие особенности:

• для отделения целой части мантиссы от дробной используется разделительная точка;

• нулевая мантисса не отображается (число начинается с разделительной точки);

• мантисса отделятся от порядка пробелом, который рассматривается как знак умножения;

• мнимая часть комплексных чисел задается умножением ее на символ мнимой единицы I (квадратный корень из -1);

• в выводе комплексного числа знак умножения на I заменяется пробелом.

Десятичная точка в числах имеет особый статус: указание ее в любом месте числа, а также в конце, делает число вещественным и ведет в переводу вычислений в режим вычислений с вещественными числами. При этом количеством выводимых после десятичной точки цифр можно управлять, задавая их значение системной переменной Digits:

> restart;

> 12/5;

12/5 > 12./5;

2.400000000

> 12/5.;

2.400000000 > Digits:=3;

Digits := 3 > 12345678/7.;

7 .17610

> Digits:=30;

Digits := 30 > 12345678/7.;

7 .176366828571428571428571428571 10

> Digits:=10;

Digits := 10 > ln(2.);

.6931471806

Для работы с числами Maple V имеет множество функции. Они будут рассмотрены в дальнейшем.

9.2.2. Контроль за числами

Числа могут служить объектами ввода, вывода и константами, входящими в математические выражения. Функция type(x, numeric) позволяет выяснить, является ли х числовой константой. Если да, то функция возвращает логическое значение true (ИСТИННО), а если нет, то — false (HE ИСТИННО). Например:

> type(10, numeric);

true > type(0.01, numeric);

true > type(Pi, numeric):

false > type(4/3, numeric);

true > typefx^, numeric);

false

Функцию type(x, integer), type(x, racional) и type(x, fraction) можно использовать для оценки того, имеет ли х значение соответственно целого числа, рационального числа или простой дроби.

9.2.3. Преобразования чисел с разным основанием

Возможна работа с числами, имеющими различное основание (base), в частности, с бинарными числами (основание 2 — binary), восьмеричными (основание 8 — octal) и шестнадцатеричными (основание 16 — hex). Функция convert позволяет легко преобразовывать форматы чисел:

>X:=1^34b;

x := 12345 > b:=convert(x,binary);

b:=11000000111001 > o:=convert(x, octal);

о := 30071 > h:=convert(x,hex);

h := 3039 > convert(h, decimal, hex);

12345 > convert(o, decimal, octal);

12345 > convert(b, decimal, binary);

12345

Помимо приведенных форм функция convert имеет ряд других. С ними можно познакомиться с помощью справки по этой мощной функции. В дальнейшем будет приведен ряд других применений этой функции.

9.2.4. Строковые данные

Строки как тип данных — это просто цепочки символов. Они обычно используются для создания текстовых комментариев. Строки должны каким-либо образом выделяться, с тем чтобы Maple-язык не отождествлял их с именами констант и переменных. Для этого строки-комментарии имеют внутренний разделительный признак, который устанавливается при их вводе в строке ввода (нажатием клавиши F5 с исчезновением знака >). В других случаях последовательность символов рассматривается как строка, если она заключена в обратные апострофы, т.е. значки '. Два апострофа подряд формируют апостроф как знак символьной строки, например 'abc"def дает строку abc'def. Любое математическое выражение может входить в строку и, разумеется, оно при этом не выполняется:

> '2+2 не всегда "четыре"';

2+2 не всегда 'четыре'

Кроме того, любой текст строки после знака # рассматривается как невыводимый строчный комментарий, даже если это математическое выражение. При этом он не вычисляется. Например:

> 2+3; # Это пример 4+5;

В данном случае строка «Это пример 4+5:» не выведена в область вывода и ее можно рассматривать как программный комментарий, не выводимый при ее исполнении, но видимый при просмотре документа.

9.2.5. Списки, массивы, векторы и матрицы

Как отмечалось, важным типом данных являются списки (lists). Они создаются с помощью квадратных скобок, например:

Типы данных 111

[1,2,3,4] — список из четырех целых чисел;

[1.,2.34,5] — список из двух вещественных и одного целого числа;

[а,Ь,'Привет'] — список из двух символов (переменных) и строковой константы;

[sin(x), 2*cos(x),a'2-b] — список из трех математических выражений.

Для создания векторов (одномерных массивов) и матриц (двумерных массивов) служит функция array. Обычно она используется в форме:

array[a..b,sl] — возвращает вектор с индексами от а до Ь и значениями в

одномерном списке si;

array[a..b,c..d,s2] — возвращает матрицу с номерами строк от а до Ь, столбцов

от с до d и значениями в двумерном списке s2.

Примеры задания вектора и матрицы представлены ниже:

array(1..3,[x,y,x+yj) — создает вектор с элементами х, у и х+у

array(1..2,1..2,[[a,b],[c,d]]) — квадратная матрица а ,

Двумерные списки часто путают с матрицами. Следует помнить, что векторы и матрицы создаются с помощью функции array и являются отдельным типом данных. Элементами векторов и массивов могут быть константы, переменные, выражения, списки и иные объекты. Эти элементы являются индексированными переменными, и их положение указывается индексами.

Имеется множество функций для работы со списками, массивами и матрицами. Они будут рассмотрены в дальнейшем. В принципе размерность массивов, создаваемых списками, не ограничена и массивы могут быть многомерными.

9.2.6. Таблицы

Еще одним важным типом данных являются таблицы. Они задают множественные данные с произвольной индексацией. Для создания таблиц служит функция table, которая в простейшем виде table() создает шаблон пустой таблицы:

> table();

table([

])

Пустая таблица резервирует память под данные. Когда параметром функции table является список выражений, он выводится в естественном порядке расположения элементов таблицы, но с произвольным порядком индексации:

>table([12,34,5,x,y+z]);

table([

3=5

4=х

5=y+z

1 = 12

2=34

])

> S:=table([(one)=1 ,(two)=2,(three)=3]);

S := table([

one = 1

three = 3

two = 2

1) > S[1];

S[1] > S[three];

3 > S[one];

1 > entries(S);

[3], [2],[1] > indices(S);

[three], [two], [one]

В конце приведенных примеров показано, как можно выделить отдельные компоненты таблицы и вывести значения и индексы таблицы с помощью функции entries и indices. Следующие примеры показывают, что таблицу можно использовать для выполнения математических преобразовании:

> F := table([sin=cos,cos=-sin]):

> op(op(F));

[cos = -sin, sin = cos] > F[cos](Pi/2);

-1

> F[sin](0);

1 > evalf(cos(Pi/2));

0 > evalf(sin(O));

Следует внимательно присмотреться к этим примерам, они демонстрируют замену функции косинуса на отрицательный синус, а синуса — на косинус.

9.3. Константы 9.3.1. Числовые константы

Константы — это простейшие поименованные объекты, несущие заранее предопределенные значения. Их имена (идентификаторы) также заранее определены в системе и не могут меняться. Подробную информацию о константах можно найти, исполнив команду ?constant.

Числовые константы не имеют имени и представлены просто числами, типы которых указаны выше. Можно считать, что именем такой константы является само ее значение. Например, в выражении 2*sin(1.25) числа 2 и 1.25 являются числовыми константами. При этом указание десятичной точки делает константу действительным числом, например, 2 — это целочисленная константа, а 2. или 2.0 или 1.25 — это уже действительные константы.

Константы 113

9.3.2. Строковые константы

Строковыми константами являются произвольные цепочки символов, заключенные в обратные апострофы, например, 'Hello', 'Привет', 'My number' и т.д. Числа, заключенные в апострофы, например, '123456', также становятся строковыми константами, и подобные константы нельзя использовать в арифметических выражениях. Строковые константы представляют значения строковых переменных. В строковых константах можно использовать символы кириллицы при условии, что имеются соответствующие наборы шрифтов.

9.3.3. Встроенные в ядро константы

Есть также ряд констант, которые правильнее считать заведомо определенными глобальными переменными:

false — логическое значение «НЕ ИСТИННО»;

gamma — константа Эйлера, равная 0.5772156649..;

infinity — положительная бесконечность (отрицательная задается как -infinity);

true — логическое значение «ИСТИННО»;

Catalan — константа Каталана, равная 0.915965594.. FAIL — специальная константа (см. ?FAIL);

I — мнимая единица (квадратный корень из -1);

Pi —константа р=3.141....

Любопытно, что в этот список не входит основание натурального логарифма — число е. В качестве этой константы рекомендуется использовать ехр(1). Оно отображается как жирная прямая буква е. A exp(l.O) выводит 2.71828... (что и следовало ожидать).

9.3.4. Идентификация констант

Функции type(x, constant) и type(x, realcons) возвращают логическое значение true, если х представляет целочисленную или вещественную константу, и false, если х не является константой. Таким образом, эти функции можно использовать для идентификации констант, например:

> type(2, constant);

true > type(0.0025, constant);

true > type(ln(-Pi),constant);

true > type(infinity.constant);

true > typefx^, constant);

false > type(4, realcons);

true > type(3+2"l, realcons);

false

114 Основные понятия входного языка системы Maple V

> type(23.5, realcons);

true

> type(ln(Pi), realcons);

true > type(sin(2), realcons);

true > type(infinity, realcons);

true

> typetx^, realcons);

false

Имена встроенных констант (как и имена функции) защищены специальным атрибутом protected. Поэтому (без его снятия) константам нельзя присваивать какие-либо значения:

>Pi;

>Pi:=1;

Error, attempting to assign to 'Pi' which is protected

> gamma;

gamma

> gamma:=10;

Error, attempting to assign to 'gamma' which is protected

Стоит упомянуть о такой экзотической возможности, как задание в Maple V собственных констант, путем описания алгоритма генерации входящих в константу цифр (это позволяет получать в представлении константы любое число цифр). Большинство пользователей довольствуется применением вместо таких констант обычных переменных подходящего типа. Зато пользователи-истинные математики соревнуются друг с другом в создании все новых и новых констант и алгоритмов их вычислении.

9.4. Переменные 9.4.1. Типы переменных

Как следует из самого названия, переменные — это объекты, значения которых могут меняться по ходу выполнения документа. Пока мы рассматриваем лишь глобальные переменные, доступные для модификации значений в любом месте документа. Тип переменных в системе Maple V определяется присвоенным им значением, это могут быть целочисленные (integer), рациональные (racional), вещественные (real), комплексные (complex) или строчные (string) переменные и т.д. Переменные могут быть также символьного типа (их значением является математическое выражение) или списочного типа (см. далее). Для явного указания типа переменных используется конструкция

mame::type

Переменные 115

где: name — имя (идентификатор) переменной, type — тип переменной, например, целочисленный integer, вещественный с плавающей точкой float, со значением >=0 nonneg, комплексный complex и т.д.

9.4.2. Идентификаторы (имена) переменных

Переменные задаются своим именем — идентификатором, которое должно начинаться с буквы и быть уникальным. Это значит, что ключевые слова языка Maple нельзя использовать в качестве имен переменных. Хотя имена ряда команд и функций можно использовать в качестве идентификаторов переменных, делать это крайне нежелательно. Ограничений на длину идентификатора практически нет — точнее, она не должна содержать более 524275 символов! Так что сложностей с подбором идентификаторов для переменных нет.

Имена переменных могут содержать одну букву — например х, Y или Z, либо ряд букв — Xmin или Хтах. В любом случае имя переменной надо начинать с буквы. Некоторые символы, например знак _, могут использоваться в именах, например Var_l, Var_2. He рекомендуется, однако, вводить в имена переменных знаки, обозначающие операторы — например, а/Ь или а-Ь будет истолковано как деление а на b или вычитание из переменной а переменной Ь.

Имена могут задаваться в обратных апострофах. При этом они просто тождественны именам без апострофа:

>var1:=123;var2:='Hello';

var1 := 123 var2 := Hello

> 'var1';'var2';

123 Hello

Строчные и прописные буквы в идентификаторах различаются, так что Var1 и var1 — это разные переменные.

Для проверки предполагаемого имени на уникальность достаточно выполнить команду ?name, где: name — выбранное имя. Если при этом откроется окно справки с этим именем, значит оно уже использовано в системе. Лучше воздержаться от его применения, так как связанная с этим именем команда или функция перестает работать, как только это имя закрепляется за какой-либо переменной.

9.4.3. Присваивание переменным значений

Поскольку Maple V прежде всего система символьной математики, то по умолчанию любые переменные рассматриваются как объекты символьного типа. Благодаря этому такие переменные могут фигурировать в математических выражениях, например, таких, как sin(x)/x, без их предварительного объявления. В отличие от обычных языков программирования такое использование переменных не влечет за собой появления сообщений об ошибках и является более естественным.

Для присваивания переменным конкретных значений используется комбинированный символ «:=», например:

п:=1 — переменной п присваивается целочисленное значение 1;

х:=123.456 — переменной х присваивается вещественное значение 123.456:

116 Основные понятия входного языка системы Maple V

у:=17/19 — переменной у присваивается рациональное значение17/18;

name:='Piter' — переменной name присвоено строковое значение 'Piter';

expr=2*Pi/3 — переменной expr присвоено значение выражения 2тс/3;

V:=[1,2,3] — переменной V присвоено значение списка чисел [1,2,3];

М:=[[1,2,3],[4,5,6]] — переменной М задано значение двумерного массива;

f:=x->x'2 — переменной f задано значение функции пользователя f(x)=x^.

Правая часть выражения присваивания определяет тип переменной. Например, она может быть целочисленной, действительной, строковой, индексированной (элемент массива) и т.д.

9.4.4. Отмена операции присваивания и команда restart

Переменная, имеющая какое-либо значение, занимает в памяти намного больше места, чем неопределенная переменная. Поэтому нередко целесообразно отменить присваивание у тех переменных, которые в дальнейшем можно не использовать. Это может понадобиться и в том случае, когда какую-либо переменную с численным или иным значением нужно использовать просто как неопределенную переменную.

Рассмотрим следующий пример:

>х:=10;

х:=10

>х:

> inHx^.x);

Error, (in int) wrong number (or type) of arguments

Здесь не удалось вычислить интеграл с подынтегральной функцией х'2 из-за того, что переменная х уже определена ранее как целочисленная переменная со значением 10, тогда как для вычисления интеграла она должна быть необъявленной или строковой (убедитесь в этом сами).

Для уничтожения присваивания надо использовать следующее выражение:

> х:='х';

х := х

Итак, заключение имени переменной в прямые апострофы ликвидирует присваивание. Так что запись х:='х' означает, что переменной х возвращается статус неопределенной переменной. Теперь можно вычислить интеграл:

> in^x^.x);

3 1/3 х

Можно сделать переменную х неопределенной и с помощью выражения вида x:=evaln(x). Это поясняет следующий пример:

>х:=10;

х:= 10

> х;

> x:=evaln(x);

x := x >x;

Для отмены присваивания значении разом всем переменным (и введенным функциям пользователя) можно использовать команду restart. Следующие примеры поясняют ее применение:

>х:=10;

х := 10 > 2«xл2;

200 > restart;

>х;

> 2»xл2;

2 2х

Следует отметить, что команда restart отменяет все предшествующие определения, что иногда чревато осложнениями. Применяйте ее только тогда, когда вы уверены, что предшествующая заданной часть документа (или даже ряда документов) действительно не важна.

Важно отметить, что Maple V сохраняет в памяти все определения и присваивания, которые были сделаны во всех загруженных в систему документах. Поэтому результаты вычислений в текущем документе могут зависеть от определений в других документах. Команда restart позволяет исключить эту зависимость.

9.4.5. Придание переменным статуса предполагаемых оператором assume

В большинстве расчетов пользователей Maple V вполне удовлетворяет статус переменных, соответствующий присвоенным им значениям. Однако серьезные расчеты предполагают, что переменные могут иметь определенные признаки;

например, они не должны принимать отрицательных значений при обычном вычислении квадратного корня или логарифма числа.

Для придания переменным статуса предполагаемых используется оператор assume:

assume(x,prop);

где х: — переменная, имя или выражение, prop — свойство. Следующие примеры показывают применение оператора assume:

> restart;

> assume(x, positive);

>x;

т s:=x->sqn(x);

s := sqrt > s(2.); .

1.414213562 > s(-2);

1/2

> is(x.positive);

true

> about(x);

Originally x, renamed x~:

is assumed to be: RealRange(Open(O),infinity)

Обратите внимание, что в этом примере переменная х помечена как положительная и при выводе сопровождается знаком тильды -, что предупреждает нас о ее особом статусе. Это не означает, что она не может принять отрицательное значение. Однако с помощью функции is можно убедиться в ее особом статусе и при необходимости программным путем исключить вычисления для х<0. Кроме того, о свойствах переменной можно узнать с помощью функции about(name) .

Иногда к уже имеющимся признакам надо добавить новые. Для этого используется функция additionally:

> assume(a.nonneg);

> additionally(a<=0);

> about(a);

Originally a, renamed a~:

is assumed to be: 0

В этом примере переменной а вначале задан признак положительности, а затем а<=0. Оба признака удовлетворяются только при а=0, что и подтверждает вывод информации о статусе этой переменной функцией about(a).

Для отмены переменным статуса предполагаемых используются те же приемы, что и при отмене переменным присвоенного значения. Например, запись х:='х' отменят статус предполагаемой для переменной х.

9.5. Операторы и операнды 9.5.1. Виды операторов

Операторы во входном языке и языке программирования системы Maple V служат для конструирования выражений и применяются совместно с операндами. Имеется пять типов операторов:

binary

Бинарные операторы (двумя операндами).

unary

Унарные операторы (с одним операндом).

nullary

Нульарные операторы (без операнда — это одна, две и три пары кавычек.

precedence

Операторы старшинства (включая логические операторы).

functional

Функциональные операторы.

Операторы и операнды

119

Для просмотра операторов и их свойств можно использовать команды:

> ?operators[binary] > ?operators[unary] > ?operators[nullary] > ?operators[precedence] > ?operators[functional]

Для изучения примеров применения операторов нужно задать и исполнить команду

> ?operators[examptes]

Команда

> ?define

позволяет ознакомиться с функций define, с помощью которой можно определить

новые операторы.

9.5.2. Бинарные (инфиксные) операторы

Бинарные (инфиксные) операторы используются с двумя операндами. В ядро Maple V включено около трех десятков бинарные операторов.

Основные из них:

+

Сложение.

-

Вычитание.

*

Умножение.

/

Деление.

** или

Возведение в степень.

mod

Вычисление модуля.

$

Оператор последовательности.

,

Разделительная точка.

@

Оператор композиции.

@@

Повторение композиции.

Задание области (интервала).

:=

Присваивание.

&*

Некоммутативное умножение.

»

Разделитель выражений.

\и.

Конкатенация (объединение).

&string

Нейтральный оператор.

Примеры использования бинарных операторов:

>2+3;

5 > 2+3-10;

-5 > 2*3+5;

11 > 1+2/3;

5/3 > 7 mod 5;

2 > 2**3;

8 >ЗЛ2;

>3@2;

3 > 3@@2;

. (2) 3

>х@х;

(2) х

> х@@х;

(х)

X I

>х$5;

X, X, X, X, X

>\nt(^2.x='\.A);

> тЦх^Л

> x=1..5);'h'ghlj'ghlj';lg'hl'gh

124/3

> S:='Hello'.' my friend!';

S := Hello my friend!

Оператор композиции @@ может использоваться для создания сложных функции, содержащих цепные дроби:

>f:=a->1/(1+a);(f@@3)(a);

1 f := а -> —-—

1 +а

1 1

1 1 + „——

1 +а

> f(5);

1/6

>g:=a->1/(H-aл2);(g@@3)(a);

1 д := а -> -—-—

1 +а

1 / 1 \ 2

I 2 2 ¦

\ (1 +а ) /

> 9(2);

1/5

9.5.3. Операторы объединения, пересечения и исключения для множеств

Бинарные операторы union, intersect и minus определены для множеств:

union

Включает первый операнд (множество) во второй.

intersect

Создает множество, содержащее общие для операндов элементы.

minus

Исключает из первого оператора элементы второго.

В любом случае в результирующем множестве повторяющиеся элементы устраняются.

Действие этих операторов поясняют следующие примеры:

> {a,a,b,c,c,d} union {e,e,f,g};

{a, b, d, с, е, f, g} > {a,a,b,c,c,d} intersect {a,c,e,f,f,g};

{a.c} > {a,a,b,c,c,d} minus {a,d};

{b,c}

Напоминаем, что эти операторы заданы ключевыми словами.

9.5.4. Унарные арифметические операторы

Унарные операторы используются с одним операндом. Они могут быть префиксными, если оператор стоит перед операндом, и постфиксными, если он стоит после операнда.

К унарным арифметическим операторам относятся следующие семь операторов:

+

Унарный плюс (префикс).

-

Унарный минус (префикс).

!

Факториал (постфиксный).

Десятичная точка (префикс или постфикс).

$

Последовательность (префикс).

not

логическое отрицание (префикс).

%

Метка (префикс).

Примеры применения унарных операторов:

> -х;

-х > х+(-х);

> х+(+х);

2х

> 100!;

9332621544394415268169923885626670049071596826438162146859296389\5217599993 229915608941463976156518286253697920827223758251185210\ 916864000000000000000000000000

>.125;

.125

> 125.-

125.

9.5.5. Логические операторы

Логические (или Булевые) операторы указывают на логическую связь величин (или выражений). Прежде всего они представлены следующим рядом бинарных операторов:

<

Менее чем.

<=

Менее чем или равно.

>

Более чем.

>=

Более чем или равно.

=

Равно.

о

Не равно.

and

Логическое И.

or

Логическое ИЛИ.

Конструкции с этими операторами (например х=у) возвращают логическое значение true, если условие выполняется, и false, если оно не выполняется.

Кроме того, к логическим относится унарный оператор not — он представляет логическое НЕТ. Для возврата логических значений выражений с этими операторами используется функция еуа1Ь(условие), например:

>2=2;

2=2 > evalb(");

true > evalb(2<>2);

false > evalb(not(true));

false >evalb(2=2and3>1);

true >eval(2=2or3<1);

true > evalb(x*y=y*x);

true

Логические операторы часто используются в управляющих структурах программ, составленных на языке программирования системы Maple V. Такое применение мы рассмотрим позже.

9.5.6. Специальные типы операторов

Операторы в Maple V описывают операции по преобразованию данных, в частности выражений. В свою очередь их можно отнести к данным абстрактного типа.

Могут быть описаны следующие типы операторов:

Операторы и операнды

123

• неопределенные (0;

• нейтральные (&);

• процедурные;

• функциональные;

• композиционные (@).

Оператор относится к неопределенным, если он не был заранее определен. Такой оператор не выполняет никаких действий и просто повторяется в строке вывода:

>f(1,2,a);

f(1,2,a)

Композиционные операторы (на базе знака @) уже описывались. Другие типы операторов рассмотрены ниже.

9.5.7. Функциональные операторы

Функциональные операторы Maple-языка являются альтернативами функций и записываются в двух формах:

Нотация

Запись оператора

"arrow" (стрелочная)

vars -> result

"angle bracket" (в угловых скобках)

<result ¦ vars>

Вторая форма задания функционального оператора имеется только в ранней версии Maple V R3.

Они могут использоваться для реализации подстановок. Например, запись х -> х'2 или < х*2 ¦ х >

означает подстановку х*2 на место переменной х. Возможны и такие подстановки в множественной форме:

(х,у) -> х"2 + у"2 х -> (2*х, 3*x^4) (x,y,z) -> (х*у, y*z)

Ниже приведены примеры работы с функциональными операторами, записанными во второй форме (только для Maple V R3):

> F := <sin(x)¦x>;

F := sin

> F(t);

sin(t) >A:=<1>;

A:= 1

><1>(x);

> 1(х);

>В:=<3.14>;

В:=3.14

> <3.14>(х,у);

3.14 > 3.14(х,у);

3.14 > <x>(t);

t > (a+b)(t);

a(t) + b(t) >(a+1)(t);

a(t) + 1 >(<in(x)+1>@@2)(t); .

ln(ln(t)+ 1)+ 1 > ( <sin(x)>@<arcsin(x)> )(t);

Функциональный оператор в Maple V часто используется для задания функции пользователя, что будет рассмотрено несколько позднее.

9.5.8. Нейтральные операторы, определяемые пользователем

Для создания нейтральных операторов, определяемых пользователем, служит знак амперсанда &. Синтаксис нейтрального оператора следующий:

&name

Имя оператора строится по правилам задания допустимых идентификаторов. Однако в имени не должны быть цифры и следующие символы и слова:

& I(){}[]::''# <ENTER> <SPACE>

Максимальная длина имени 495 символов. Нейтральные операторы могут быть унарными и бинарными. Пример задания бинарного нейтрального оператора приведен ниже:

> х&/у;

х&/у > z+xS/y;

z + (х &/ у)

> &/(х.у);

х&/у

> х&/у-&/(х,у);

о 9.5.9. Определение операторов с помощью оператора define

Большие возможности в задании операторов с заданными свойствами предоставляет специальный оператор define. Он записывается в форме:

define(aa(oper)) или define(oper, propertyl, property2, ...)

Операторы и операнды 125

Здесь орег — имя определяемого оператора, аа — имя абстрактного алгебраического пространства (группового Group или линейного Linear), property I, proper-ty2,... — наименование свойства. В принципе оператор define позволяет создавать операторы с новыми свойствами, которые отсутствуют у операторов и функций, встроенных в систему.

Могут быть указаны следующие свойства операторов:

unary — унарный оператор;. binary — бинарный оператор;

associative — ассоциативный оператор f(x,f(y,z)) = f(f(x,y),z) = f(x,y,z);. commutative или symmetric — коммутативный симметричный оператор f(x,y) = f(y,x):

antisymmetric — асимметричный оператор f(x,y) = -f(y,x);

inverse=g — инверсный оператор;

zero=x — определение нуля — если любой из элементов оператора равен х, то оператор возвращает х;

identity=x — определение бесконечности.

Следующий пример задает линейный оператор L:

> define(Linear(L));

> Ua'x+b'x^+c'x^);

2 3 L(ax)+L(bx )+L(cx )

Для задания некоторых свойств операторов можно использовать уравнения и соотношения вида f(x)=value. Чтобы свойство выполнялось для всех аргументов (или некоторого класса аргументов), используется описатель forall. Так, приведенный ниже пример задает оператор F, который вычисляет п-е число Фибоначчи (п>2):

> define(F, forall(integer(x), F(x) = F(x-1)+F(x-2)), F(0)=0, F(1)=1);

> F(3);

2 > F(4);

3 >F(10);

> F(20);

6765 > time(F(20));

3.228

Обратите внимание на то, что здесь описателем forall задана целочисленная переменная х. А соотношения F(0)=0 и F(1)=1 задают начальные значения массива чисел Фибоначчи, которые нужны для реализации обычного итерационного алгоритма их нахождения. Напоминаем, что очередное число Фибоначчи равно сумме двух предшествующих чисел Фибонначи.

Последний пример иллюстрирует применение системной функции time для определения времени, затраченного на вычисление значения функции F(20). Это

126 Основные понятия входного языка системы Maple V

время задается в секундах. Нетрудно заметить, что даже для ПК с процессором Pentium 200 ММХ это время оказалось довольно значительным (более 3 с), поскольку каждое новое число Фибоначчи вычисляется заново.

9.6. Математические функции

Maple V имеет полный набор элементарных математических функции. Все они, кроме арктангенса двух аргументов, имеют один аргумент х, например sin(x). Он может быть целым, рациональным, дробно-рациональным, вещественным или комплексным числом г. В ответ на обращение к ним элементарные функции возвращают свое соответствующее значение. Поэтому они могут быть включены в математические выражения.

Как правило, если аргументом функции является фундаментальная константа, целое или рациональное число, то функция выводится с таким аргументом без получения результата в форме действительного числа с плавающей точкой. Например:

> Sin(Pi);

Sin(Pi) >ехр(1);

ехр(1) > Ш(2);

ln(2) >arosin(1/3);

arcsin(1/3) >arcsin(1/2);

1/6 Pi

Нетрудно заметить, что есть и исключения из этого правила — например, на экране дисплея ехр(1) будет выведено как константа е, а значение функции arcsin(l/2) все же вычислено и результат получен как 1/6 от константы Pi. Вообще говоря, если результат просто выражается через фундаментальную константу, то он будет вычислен и представлен ею.

Для получения подробной информации о некоторой произвольной функции <f> достаточно задать команду

?<f>

Ввиду общеизвестности элементарных функций мы не будем обсуждать ни их свойств, ни допустимых пределов изменения аргумента. Приведем перечень наименований этих функций, представленный по различным их категориям с примерами применения некоторых функций.

9.6.1. Некоторые целочисленные функции и факториал

Ниже представлены наиболее распространенные целочисленные функции Maple V, используемые в теории чисел:

factorial

Функция вычисления факториала (альтернатива — оператор !).

iquo(a,b)

Частное для а/Ь.

Математические функции

127

irem(a,b)

Остаток для a/b.

igcd(a b)

Наибольший общин делитель.

lcm(a.b)

Наименьшее общее кратное.

Примеры применения:

>factorial(10);

3628800

> factorial 100);

9332621544394415268169923885626670049071596826438162146859296389\5217599993 229915608941463976156518286253697920827223758251185210\ 916864000000000000000000000000

> iquo(123,5);

24 > irem(123,5);

3 > igcd(1240,24);

>lcm(13,7);

>30!;

265252859812191058636308480000000 >3!!;

720

> (3!)';

720

В последних двух примерах применения оператора факториала полезно обратить внимание, что запись п!! означает лишь (п!)!, а не п!!=2*4*6*..., т.е. произведение четных целых чисел.

9.6.2. Тригонометрические функции

В Maple-языке в ядре определены следующие тригонометрические функции:

sin

Синус.

CSC

Косеканс.

sec

Секанс.

tan

Тангенс.

cos

Косинус.

cot

Котангенс.

Примеры вычислений:

> simpli^sintx^+costx)^);

>sin(1.0);

.8414709848

> arctan(:!'.,J);

.5880026035

9.6.4. Гиперболические функции

Гиперболические функции представлены следующим набором:

sinh

Гиперболический синус.

seen

Гиперболический секанс.

cosh

Гиперболический косинус.

csch

Гиперболический косеканс.

tanh

Гиперболический тангенс.

coth

Гиперболический котангенс.

Примеры применения:

>sinh(1.);

1.175201194 > cosh(1);

cosh(1) >tanh(2.);

.9640275801 >coth(1.);

1.313035286

9.6.5. Обратные гиперболические функции

Как и тригонометрические функции, гиперболические имеют свои обратные функции, называемые ареафункциями:

arcsinh

Гиперболический арксинус.

arcsech

Гиперболический арксеканс.

arccosh

Гиперболический арккосинус.

arccsch

Гиперболический арккосеканс. ,

arctanh

Гиперболический арктангенс.

arccoth

Гиперболический арккотангенс.

Примеры применения:

> arcsin(2+3.*l);

.5706527843 +1.983387030 I >arccos(1.);

О > arctan(1.);

.7853981634 > arcsech (2.);

1.047197551 I

9.6.6. Алгебраические функции

К алгебраическим относятся следующие функции системы Maple V:

ехр

Экспоненциальная функция.

iloglO

Целочисленный логарифм по основанию 10.

130

Основные понятия входного языка системы Maple V

ilog

Целочисленный логарифм (библиотечная функция).

In

Натуральный логарифм.

log

Логарифм по заданному основанию (библиотечная функция).

loglO

Логарифм по основанию 10.

sqrt

Квадратный корень.

Примеры применения:

> ехр(2);

ехр(2) > ехр(2.0);

7.389056099 >ilog10(1000);

3 > readlib(ilog);

proc(x)... end >ilog[2](100);

6 > ln(2.);

.6931471806 >log(100);

ln(100) > log(100.);

4.605170186 > log[10](100.):

2.000000000 > log[2](9);

ln(9)

ln(2) > readlib(log10);

proc(x)... end >log10(1000.);

3.000000000 > evalc(sqrt(2+3"l));

1/2 1/2 1/2 1/2 1/2(4+2 13 )+1/2 1(4+2 13 )

>sqrt(10+90.);

10.00000000

9.6.7. Функции с элементами сравнения

В алгоритме вычисления ряда функций заложено сравнение результата с некоторым опорным значением. К таким функциям относятся:

Математические функции

ceil

Наименьшее целое, большее или равное х.

floor

Наибольшее целое, меньшее или равное х.

frac

Дробная часть числа.

trunc

Меньшее целое, округленное в направлении х=0.

round

Округленное значение числа.

signum

Функция знака (-1 при х<0, 0 при х=0 и +1 при х>0).

Для комплексного аргумента х между этими функциями существуют следующие соотношения:

trunc(x) = trunc(Re(x)) + I*trunc(Im(x));

round(x) = round(Re(x)) + I*round(Im(x));

frac(x) = frac(Re(x)) + I*frac(Im(x)).

Для floor(x) запишем a = Re(x)-floor(Re(x)) и b = Im(x)-floor(Im(x)). Тсгда floor(x) = floor(Re(x)) + I*floor(Im(x)) + X, где:

О если a+b < 1

X = 1 если a+b > 1 и а > b

I если a+b > 1 и а < b и

ceil(x) = -floor(-x). Примеры применения:

> ceil(Pi);

4 > trunc(Pi);

3 > floor(Pi);

3 > frac(Pi);

Pi-3 > frac(evalf(Pi));

.141592654 > round(Pi);

3 > ceil(-Pi);

-3 > trunc(-Pi);

-3 > trunc(2.6+l*3.4);

2+31

> floor(-Pi);

-4

> floor(3.7-4.2*l);

3-4 > round(-Pi);

> signum(Pi);

> signum(O):

> signum(-5);

9.6.8. Функции комплексного аргумента

Для комплексных чисел и данных, помимо упомянутых в предшествующем разделе функции, определен следующий ряд базовых функций:

abs

Абсолютное значение действительного или комплексного числа.

argument

Аргумент комплексного числа.

conjugate

Комплексно-сопряженное число.

Im

Мнимая часть комплексного числа.

Re

Действительная часть комплексного числа.

polar

Полярное представление комплексного числа (библиотечная функция).

max

Максимальный по значению элемент списка.

min

Минимальный по значению элемент списка. '!Q

Примеры применения:

>z:=2+l*3;

z:=2+31 > abs(z);

1/2 13

> argument(z);

arctan(3/2) > conjugate(z);

2-31 > lm(z);

3 > Re(z);

> readlib(polar);

proc(r, th)... end

> polar(z);

1/2

polar(13 , arctan(3/2)) > polar(-3,Pi/2);

polar(3, 3/2 Pi) > min(Pi/2,Pi,2*Pi);

1/2 Pi > max(Pi/2,2"Pi,Pi);

2 Pi >sort([2,1,3]);

[1,2,3]

Обратите внимание, что при выводе значении факториальной функции в виде

больших чисел используется знак перевода на следующую строку \. Встречая такой знак, надо мысленно его игнорировать, так что записанное многострочное число является одним целым.

9.6.9. Специальные математические функции

Специальные математические функции обычно являются решениями линейных дифференциальных уравнений различного типа и имеют представления в виде интегралов, не представимых через элементарные функции. Maple V имеет практически полный набор таких функций. Их представления можно найти в справочной литературе, а также в справочной базе системы. В связи с этим ограничимся приведением названий специальных функций:

AiryAi (Bi)

Функции Эири.

AngerJ

Функция Ангера.

bernoulli

Числа и полиномы Бернулли.

Bessell (J, K, Y)

Функции Бесселя разного рода.

Beta

Бета-функция.

binomial

Биноминальные коэффициенты.

Chi

Интегральный гиперболический косинус.

Ci

Интегральный косинус.

csgn

Комплексная сигнум-функция.

dilog

Дилогарифм.

Dirac

Дельта-функция Дирака. . . ,

Ei

Экспоненциальный интеграл.

EllipticCE (CK, CPi, E, F, K, Modulus, Nome, Pi)

Эллиптические интегралы.

erf

Функция ошибок.

erfc

Дополнительная функция ошибок.

euler

Числа и полиномы Эйлера.

FresneIC (f,g,S)

Интегралы Френеля.

134

Основные понятия входного языка системы Maple V

GAMMA

Гамма-функция.

GaussAGM

Гаусса арифметико-геометрическое среднее.

HankelHl (H2)

Функции Ханкеля.

harmonic

Частичная сумма серии гармоник.

Heaviside

Функция Хевисайда.

JacobiAM (CN. CD, CS, DN,DC,DS, NC, ND,NS,SC, SD, SN)

Эллиптические функции Якоби.

JacobiThetal (2, 3, 4)

Дзета-функции Якоби.

JacobiZeta

Зет-Функция Якоби.

KelvinBer (Bei, Her, Hei, Ker, Kei)

Функции Кельвина.

Li

Логарифмический интеграл.

InGAMMA

Логарифмическая Гамма-функция.

MeijerG

Меиера G-функция.

pochhammer

Символ Постмайера.

polylog

Полилогарифмическая функция.

Psi

Полигама-функция.

Shi

Синусный гиперболический интеграл.

Si

Интегральный синус.

Ssi

Синусный интеграл смещения.

StruveH (L)

Функции Струве.

surd

Не главная корневая функция.

LambertW

Ламберта W-функция.

WeberE

Вебера Е-функция.

WeierstrassP

Р-функция Вайерштрассе.

WeierstrassPPrime

Производная Р-функции Вайерштрассе.

WeierstrassZeta

Зета-функция Вайерштрассе.

WeierstrassSigma

Сигма-функция Вайерштрассе.

Zeta

Зета-функция Римана и Гурвица.

Ввиду большого числа специальных функций, ограниченности их применения и наличия множества примеров на их вычисления в справочной системе Maple V ограничимся несколькими примерами на вычисления наиболее распространенных специальных функций.

Примеры применения:

> eq1 :=xл2•diff(y(x),x$2)+x«diff(y(x),x)+(xл2-pл2)*y(x)=0;

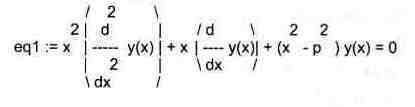
> a1:=dsolve(eq1,y(x));

a1 := у(х) = _С1 BesselY(p, x) + _С2 BesselJ(p, x)

> BesselJ(0,0.5);

.9384698072 > GAMMA(0.5);

1.772453851 > diff(BesselJ(p,x),x$2);

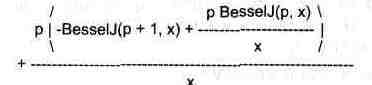
>Ei(1.);

1.895117816 > diff(FresnelS(x),x$3);

2 22 2

-sin(1/2Pix ) Pi x +cos(1/2Pix ) Pi

Еще несколько примеров работы со специальными функциями представлено на рис. 9.2. Как видно из этого примера, представление в математически ориентированном виде на экране дисплея более предпочтительно, чем на Maple-языке. Записи функции при этом выглядят как в обычной математической литературе.

Рис. 9.2. Примеры работы со специальными математическими функциями.

136 Основные понятия входного языка системы Maple V

Подробное описание специальных функции можно найти в справочниках [43 -45] и в справочной базе данных системы Maple V.

9.6.10. Функции для работы с векторами и матрицами

Свыше сотни функций для работы с векторами и матрицами входит в пакет расширения системы Maple V linalg (линейная алгебра). Он описан в главе 12. В связи с этим в ядро и в основную библиотеку Maple V включено ограниченное число средств для работы с векторами и матрицами. Они описаны ниже.

Прежде всего надо отметить, что элементы векторов и матриц являются индексированными переменными, т.е. место каждого элемента вектора определи ется его индексом, а у матрицы — двумя индексами. Обычно их обобщенно обозначают как i (номер строки матрицы или порядковый номер элемента вектора) и j (номер столбца). Допустимы операции вызова нужного элемента и присваивания ему нового значения:

V[i] — вызов i-го элемента вектора V;

M[i,j] — вызов элемента матрицы М, расположенного на i-строке j-столбце;

V[i]:=x — присваивание нового значения х i-му элементу вектора V;

M[i,j]:=x — присваивание нового значения х элементу матрицы М.

Следующие примеры иллюстрируют работу с элементами векторов и матриц:

>V:=array(1..3,[1,2,3]);

V:= [1,2,3] >V[1]:=a:V[3]:=b:

> evalm(V);

[a, 2, b] >M:=array(1..3,1..3,[[a,b,c],[d,B,f],[i,k,l]]);

[a b c]

[ ] [d e f]

[ ] [i k I]

> М[2,2]:='Привет':

> evalm(M);

[a b c]

[ ] [d Привет f]

[ 1 [i k I]

> M[3,2];

k > M[2,2];

Привет > type(V.vector);

true > type(M,vector);

false

> type(M,matrix);

true

В этих примерах применены еще две функции для работы с векторами и матрицами — evalm и type (с опциями vector и matrix):

evalm(M) — эволюция матрицы М;

type(V, vector) — тестирует вектор V и возвращает true, если V — вектор,

и false — в ином случае;

type(M, matrix) — тестирует матрицу М и возвращает false, если М — матрица,

и false — в ином случае.

К векторным и матричным функциям можно также отнести функцию преобразования convert с опциями vector и matrix:

>М1:=[1,2,3,4);

М1 •=[1,2, 3,4] > type(M1, vector);

false > V:=convert(M1, vector);

V:=[1,2,3,4] > type(V,vector);

true >M2:=[[1,2],[3,4]];

M2:=[[1,2],[3,4]] > type(M2, matrix);

false ' M:=convert(M2,matrix);

[1 2] M:=[ ] [3 4]

' type(M, matrix);

true

Z матрицами одинакового размера можно выполнять типовые операции сложения,

!ычитания, умножения, деления и возведения в степень. Возможны также юдобные операции с матрицей и скаляром.

1римеры описанных операций представлены ниже:

•M1:=array(1..2,1..2,[[a1,b1],[c1,d1]]);

[а1 Ь1] М1:=[ ] [с1 d1]

•M2:=array(1..2,1..2,[[a2,b2],[c2,d2]]);

[а2 b2] М2 := [ ] [с2 d2]

>evaim(Mi+M^);

[a1 + a2 b1 + b2]

[ I

[c1 + c2 d1 + d2]

>evalm(M1-M2);

[a1 - a2 b1 - b2]

[ ] [c1-c2 d1-d2]

>evalm(M1&'M2);

[a1 a2 + b1 c2 a1 b2 + b1 d2]

[ ] [c1 a2 + d1 c2 c1 b2 + d1 d2]

> evalm(M1/M2);

a1 d2 b1 c2 a1 b2 b1 a2 ]

a2 d2 - b2 c2 a2 d2 - b2 c2 ' a2 d2 - b2 c2 a2 d2 - b2 c2 ]

]

c1 d2 d1 c2 c1 b2 d1 a2 ]

a2 d2 - b2 c2 a2 d2 - b2 c2 ' a2 d2 - b2 c2 a2 d2 - b2 c2 1

>evalm(M1л2);

I 2 ]

[a1 + b1 c1 a1 b1 + b1 d1]

[ ]

[ 2]

[c1 a1 +d1 c1 b1 c1 +d2 ]

>evalm(sin(M1));

[sin(a1) sin(b1)]

[ I

[sin(c1) sin(d1)]

>evalm(M1+z);

[a1 + z b1 ]

[ ] [ c1 d1+z]

>evalm(M1-z);

[a1 - z b1 ]

[ ] [ c1 d1 -z]

>evalm(M1"z);

[za1 zb1]

[ ] [zc1 zd1]

> evalm(M1/z):

[a1 b1 ]

[z z

[ [c1 d1

[--[z z

Функции для работы со строковыми данными

139

Примеры работы с матрицами, элементы которых представлены выражениями, показаны на рис. 9.3.

Я File Ed» VB>» tos«* fams flpfcre йш*» H* .alaJ.2] [ Операции с матрицами, имеющими символьные элементы ,±¦ > и: linalc¦(mati-i-x] (2, 2. (ж и, х"2-х+5, ехр(х) , sin(x'li) ] ) ; —I

.J———2-5] , :;

X . , П-,

Le ?m(y ) J > map(dlff,A,x) ,:

п х п ——— 2 х ~ 1

, й- » л- соз(.т ) -т ^ е ———————— :•-

L х [> map(int , ''.х) •

> nirfp (sili, Л) ;

sinfx ) sin('A — ,т + 5) 1зш( е ) зт( Ет(д ))

Г> _____________ттпги-гштиим.г- ^

'¦8Па™¦ ByMgoioliWad-Cha ^^М»;1»'УН<<мм<<{к^^ИИЯЙ¦¦ИЯИ^^ЬД-_МЯ_..

Рис. 9.3. Примеры работы с матрицами с элементами-выражениями.

Здесь полезно обратить внимание на применении функции тар, которая прикладывает заданную операцию (функции дифференцирования diff и интегрирования int) к каждому элементу матрицы. В результате возвращаются матрицы, каждый элемент которых представлен производной или интегралом. Аналогично над матрицами можно выполнять и другие достаточно сложные преобразования.

9.7. Функции для работы со строковыми данными 9.7.1. Контроль типа строковых данных

Напоминаем, что строковые данные представляются совокупностью любых символов в обратных апострофах, например, 'Привет' или '2+2'. Для контроля объектов на принадлежность к строковым данным служит функция type с опцией string:

str:='Hello';

str := Hello > type(Hello,string);

true > type(str,string);

true > type(2+3,string);

false > type('2+3',string);

true

> char:=a;

char:= a

> char:='a';

char:= a

Из приведенных примеров видно, что контроль строкового типа осуществляется не очень строго: в частности, единичные символы рассматриваются как строковые и без заключения их в апострофы. В строках могут быть символы кириллицы, но гарантии в правильности обработки таких символов нет — надо мириться с тем, что Maple V англоязычная система и ее возможности в поддержке других языков ограничены.

9.7.2. Интерактивный ввод строк

Для интерактивного ввода строк можно использовать функцию readline(filename)

задав в качестве имени файла terminal (возможно, не на всех системах) или опустив имя файла. В этом случае ввод строки осуществляется с клавиатуры ПК (терминала):

> s:=readline();

> Привет мой друг!

s := Привет мой друг!

Полезно обратить внимание на то, что запрос в ходе интерактивного ввода может быть сделан на русском языке, если установленный для запросов шрифт имеет символы кириллицы.

9.7.3. Обработка строк

Имеется ряд функций для работы со строками. Из них наиболее важные следующие:

lenght(str)

Возвращает число символов в строке str.

substring(str,a..b)

Возвращает подстроку в виде символов от а-го до Ь-го строки str.

cat(strl,str2,...)

Возвращает строку, полученную объединением строк strl, str2,... (альтернатива — оператор конкатенации в виде точки .).

SearchText(s,str)

Дает поиск подстроки s в строке str и при его успехе возвращает номер позиции s в строке str (при отсутствии s в str возвращает 0).

Примеры применения этих функций представлены ниже:

> length(str);

6 > substring(str,1..3);

Hel > substring(str,4..5);

lo > s:=cat('Hello',' my',' friend!');

s := Hello my friend!

> ss:='Hello '.'my friend!';

ss := Hello my friend! > seq(Name.i,i=1..4);

Name1, Name2, Name3, Name4

>add(x.i,i=1..4);

x1 + x2 + x3 + x4 > SearchText(my.s);

Эти функции дают достаточно средств для обработки данных строкового типа, которые можно применять не только для создания текстовых комментариев, но и для управления в программах вычислительным процессом.

9.7.4. Преобразования строки в математическое выражение

Часто возникает необходимость в интерактивном вводе математических выражений. Для ввода с запросом выражения используется функция

readstat(promt) где promt — строка с текстовым комментарием. Пример ее применения дан ниже:

> y:=readstat('BBenMTe выражение ');

> a'x^+b;

у := а х + b

Альтернативой может стать ввод строкового выражения с последующим преобразованием его в математическое выражение с помощью функции parse:

>s:='2+3';

s := 2+3 > evaln(s);

s > parse(");

Обратите внимание на то, что функция evain не смогла вычислить строкове выражение '2+3', поскольку оно не является числовым типом данных. Однако функция parse преобразовала это выражение в числовое, что и привело к его вычислению (эволюции).

9.8. Типовые средства программирования 9.8.1. Функции пользователя

Хотя ядро Maple V R4, библиотека и пакеты расширения содержат свыше двух тысяч функций, всегда может оказаться, что именно нужной пользователю (порою довольно простой) функции все же нет. Тогда возникает необходимость в создании собственной функции, именуемой функцией пользователя.

142 Основные понятия входного языка системы Maple V

Основным средством расширения Maple-языка являются модули — процедуры. Однако на первый взгляд они сложны. Есть и более простые способы задания функции пользователя. Один из таких способов заключается просто в присвоении введенной функции (в виде выражения) некоторой переменной:

Мате:=Выражение

Этот прием фактически означает операцию присваивания. Следующие примеры иллюстрируют технику работы с такими функциями:

> m^sqrtfx^+y^);

2 2 1/2 m:=(x +y )

> х:=3;у:=4;

х:=3

у:=4

> evalf(m);

5.000000000

Заданный таким образом программный объект все же не является полноценной функцией пользователя. Прежде всего потому, что в нем используются только глобальные переменные (х и у). Их значения приходится заведомо задавать отдельно, используя операции присваивания. Подобные конструкции нельзя ввести в библиотеки Maple V.

Более гибкий способ задания полноценных функций пользователя базируется на применении функционального оператора. При этом используется любая из двух конструкций:

name:=(x,y,...)->expr или name:=<expr¦x,y,...>

Вторая из конструкций допустима только в реализации Maple V R3. После этого вызов функции осуществляется в виде name(x,y,...), где (х,у,...) — список формальных параметров функции пользователя с именем name. Переменные, указанные в списке формальных параметров, являются локальными. При подстановке на их место фактических параметров они сохраняют их значения только в теле функции ехрг. За пределами этой функции переменные с этими именами оказываются либо неопределенными, либо сохраняют ранее присвоенные им значения.

Сказанное иллюстрируют следующие примеры:

> restart:

> х:=0;у:=0;

х:=0 у:=0

> m:=(x,y)->sqrt(x''2+y"2);

2 2 m := (х, у) -> sqrt(x + у )

> m(3,4);

5 > m(3„4.);

5.000000000

> х;у;

О О

Нетрудно заметить, что при вычислении функции т(х,у) переменные хну имели значения 3 и 4, однако за пределами функции они сохраняют нулевые значения, заданные им перед введением определения функции пользователя.

Еще один способ задания функции пользователя базируется на применении функции unapply:

name:=unapply(expr,varl,var2,...) Ниже даны примеры такого задания функции пользователя:

>fm:=unapply(sqrt(xл2+yл2),x,y);

2 2 1/2 fm := (x, у) -> (x + у)

> fm(4.,3.);

5.000000000 > fe:=unapply(xA2^-yл2,x,y);

2 2 fe := (x, у) -> x + у

> fe(sin(x),cos(x));

2 2

sin(x) + cos(x)

> simplify(fe(sin(x),cos(x)));

Последний пример показывает возможность проведения символьных операции с функцией пользователя.

9.8.2. Условные выражения

Для подготовки разветвляющихся программ в Maple-язык программирования включен оператор if, позволяющий создавать следующую конструкцию:

if <Условие сравнения> then <Элементы> elif <Условие сравнения> then <Элементы>¦ else <Элементы> ¦ fi;

В вертикальных черточках ¦ ¦ указаны необязательные элементы этой конструкции. На практике чаще всего используются следующие две конструкции условных выражений:

if <Условие> then <Элементы 1> fi — если Условие выполняется, то исполняются Элементы 1, иначе ничего не выполняется;

if <Условие> then <Элементы 1> else <Элементы 2> fi — если Условие выполняется, то испольняются Элементы 1, иначе исполняются Элементы 2.

В условиях используются любые логические конструкции со знаками сравнения (<, <=, >, >=, =, о ) и логические операторы and, or и not, конструкции с которыми возвращают логические значения true и false.

Рассмотрим следующий простой пример:

>х:=-5:

> ifx<0 then print('Negative') fi;

Negative >x:=1:

> if x<0 then print('Negative') fi;

В этом примере анализируется значение х. Если оно отрицательно, то с помощью функции вывода print на экран дисплея выводится сообщение «Negative». А если х не отрицательно, то не выводится никакого сообщения. В другом примере, если х не отрицательно, то выводится сообщение «Positive»:

> х:=-5:

> if x<0 then print('Negative') else print('Positive') fi;

Negative >x:=1:

> ifx<0 then print('Negative') else print('Positive') fi;

Positive

Приведем еще один пример, показывающий особую форму задания конструкции if-then-else-fi:

> х:=-5:

> 'if'( x<0, print('Negative'), print('Positive') fi;

Negative >x:=5:

> 'if (x<0, print('Negative'), print('Positive'));

Positive

В этой конструкции вида 'if'(Условие, Выражение!, Выражение2)

если Условие выполнятся, то будет исполнено Выражение!, в противном случае будет исполнено Выражение2. Ввиду компактности записи такая форма условного выражения нередко бывает предпочтительна, хотя она и менее наглядна.

9.8.3. Циклы типа for, while и do

Зачастую необходимо циклическое повторение некоторых выражений заданное число раз или до тех пор, пока выполняется определенное условие. Maple-V имеет обобщенную конструкцию цикла, которая задается следующим образом:

¦for<name>¦ from <ехрг1> ¦ ¦to<expr3>¦ ¦by<expr2>¦ ¦ while <ехрг4> do <statement sequence> od;

Здесь name — имя управляющей переменной цикла, expri, expr2 и ехргЗ — выражения, задающие начальное значение, конечное значения и шаг изменения переменной name, expr4 — выражение, задающее условие, пока будет выполняться цикл (набор объектов между словами do и od).

Типовые средства программирования 145

В ходе выполнения цикла управляющая переменная меняется от значения ехрг! до значения ехрг2 с шагом, заданным ехргЗ. Если блок by <expr3> отсутствует, то управляющая переменная будет меняться с шагом +1 при ехр1<ехрг2. Это наглядно поясняет следующий пример:

> for i from 1 to 5 do print(i) od;

1

2

3

4

5

Он выводит значения управляющей переменной i в ходе выполнения цикла. Нетрудно заметить, что она и впрямь меняется от значения 1 до значения 5 с шагом +1.

Следующий пример показывает, что границы изменения управляющей переменной можно задать арифметическими выражениями:

> for i from 7/(2+5) to 4+1 do print(i) od;

1

2

3

4

5

А в другом примере показано задание цикла, у которого управляющая переменная меняется от значения 1 до 10с шагом 2:

> for i from 1 to 10 by 2 do print(i) od;

1

3

5

7

9

В этом случае выводятся нечетные числа от 1 до 9. Следует отметить, что выполнение цикла в обратном порядке, когда ехрг1>ехрг2 не предусмотрено. Но зато цикл можно прервать с помощью дополнительного блока while <expr4>. Цикл с таким блоком выполняется до тех пор, пока выполняется условие ехрг4 (см. пример ниже):

> for i from 1 to 10 by 2 while i<6 do print(i) od;

1

3

5

Таким образом, конструкция цикла в Maple-языке программирования вобрала в себя основные конструкции циклов for и while. Есть еще одна более специфическая конструкция цикла:

[for <name>¦ in <exprl>¦ [while <expr2>¦ do <statement sequence> od;

Здесь expri задает список значений, которые будет принимать управляющая переменная name. Цикл будет выполняться, пока не будет исчерпан список и пока выполняется условие, заданное выражением ехрг2.

Сказанное иллюстрирует следующий пример:

> for i in [1,2.5,-1,7,9] do print(i) od;

2 5 -1 7 9

> for i in [1,2,5,-1,7,9] while i>0 do print(i) od;

2 5

В цикле этого вида управляющая переменная может меняться произвольно, принимая убывающие и отрицательные значения.

Циклы могут быть вложенными. Это иллюстрирует следующий пример, создающий единичную матрицу на базе заданного массива М:

>М:=аггау(1..3,1..3);

М := аггау(1 .. 3, 1 .. 3, []) > for i to 3 do for] to 3 do M[i,j]:=0;if i=j then M[i,j]:=1 fi; od od;

> evalm(M);

[1 0 0]

[ ] [О 1 0]

[ 1 [О 0 1]

> array(1..3,1..3, identity);

[1 0 0]

[ ] [О 1 0]

[ ] [0 0 1]

Этот пример имеет не более чем познавательное значение, поскольку для

создания такой матрицы Maple V имеет опцию identity, с помощью которой функция array позволяет сразу создать единичную матрицу.

В заключении отметим, что возможна упрощенная частная конструкция цикла типа while:

while expr do statseq od;

Здесь выражения statseq выполняются, пока выполняется логическое условие expr. Пример такого цикла:

>п:=1;

п :=1

> while n<16 do n:=2*n od;

n =2 n =4 n =8 n = 16

В этом примере идет удвоение числа n с начальным значением п=1 до тех пор, пока значение n меньше 16.

9.8.4. Операторы пропуска и прерывания

Иногда бывает нужным пропустить определенный цикл. Для этого используется оператор next (следующий). Приведенный ниже пример иллюстрирует применение оператора next в составе выражения if-fi для исключения вывода значения i=-2:

> for i in [1,2,3,-2,4] do if i—2 then next else print(i) fi od;

Другой оператор break прерывает выполнение фрагмента программы (или цикла), как только он встречается в ходе ее выполнения. Его действие поясняет слегка модифицированный предшествующий пример:

> for i in [1,2,3,-2,4] do if i=-2 then break else print(i) fi od;

В данном случае при значении i=-2 произошло полное прекращение выполнения цикла. Поэтому следующее значение 4 переменной i присвоено не было и это значение на выход цикла не попало.

Любой из операторов quit, done или stop обеспечивает также прерывание выполнения текущей программы (в частности, цикла), но при этом окно текущего документа закрывается и все имеющиеся в нем определения исчезают.

9.8.5. Простейшие процедуры

Процедурами называют модули программы, имеющие самостоятельное значение. Они являются важнейшим элементом структурного программирования и служат средством расширения возможностей системы Maple V пользователем.

Процедуры имеют имя и список параметров (даже если он пустой).

Процедуры вызываются, также как встроенные функции, указанием их имени со списком фактических параметров.

Простейшая форма задания процедуры следующая:

name := ргос(Параметры)

Тело процедуры end;

Параметры процедуры задаются перечислением имен переменных, например ргос(х) или proc(x,y,z). С помощью знака :: после имени переменной можно определить ее тип, например, в объявлении prog(n::integer) сообщается, что переменная п является целочисленной.

При вызове процедуры выражением вида пате(фактические_параметры)

фактические параметры подставляются на место формальных. Несоответствие фактических параметров типу заданных переменных ведет к сообщению об ошибке и к отказу от выполнения процедуры.

148 Основные понятия входного языка системы Maple V

В качестве примера ниже приведена процедура вычисления модуля комплексного числа z — в данном случае единственного параметра процедуры:

> modc:=proc(z)

> eval^sql^Retz^+lr^z)'^))

>end;

mode := proc(z) e\/a\f(sqrt(Re(z)"2 + In^z)^)) end

Теперь для вычисления модуля достаточно задать обращение к процедуре modc(z), указав вместо z конкретное комплексное число:

> modc(3.+l"4.);

5.000000000

Нетрудно заметить, что при знаке ; после завершающего слова end текст процедуры повторяется в строке вывода (в общем случае в несколько ином виде). Если это повторение не нужно, после слова end надо поставить знак двоеточия.

9.8.6. Оператор возврата значения RETURN

Процедуры, которые возвращают значение результата в ответ на обращение к ним, во многом тождественны функциям. Будем называть их процедурами-функциями. Обычно процедура возвращает значение последнего выражения в ее теле или выражения, намеченного к возврату специальным оператором RETURN:

> modc:=proc(z) > eval^sqrHRetz^+ln^z)^)):

> RETURN(") > end:

mode := proc(z) eval^sqrtfRetz)^ + \m{z)"2}}; RETURN(") end

> modc(3.+l*4.);

5.000000000

Параметром RETl 'RN может быть любое выражение.

9.8.7. Статус переменных в процедурах и циклах

Переменные, которые указываются в списке параметров (например, z в нашем примере), являются локальными переменными. Это означает, что изменение их значений происходит лишь в теле процедуры, т.е. локально. За пределами тела процедуры эти переменные имеют то значение, которое у них было до использования процедуры. Это хорошо поясняет следующий пример:

> restart; z:=1; .

z:= 1

> modc:=proc(z) ;• eval^sqrttRetz^+lmfz)^)):

>end;

mode := proc(z) evalf(sqrt(Re(z)л2 + lm(z)"2)) end

> modc(3.+l''4,);

5.000000000 > z;

Нетрудно заметить, что внутри процедуры z=2+I*4, тогда как вне нее значение г=\. Таким образом, имена переменных в списке параметров процедуры могут совпадать с именами глобальных переменных, используемых за пределами процедуры.

Переменные, которым впервые присваивается значение в процедуре, также относятся к локальным. Кроме того, переменные, применяемые для организации циклов, являются локальными. Все остальные переменные — глобальные.

9.8.8. Объявления переменных локальными с помощью оператора local

Если в теле процедуры имеются операции присваивания для ранее определенных (глобальных) переменных, то изменение их значении в ходе выполнения процедуры создает так называемый побочный эффект. Он способен существенно изменить алгоритм решения сложных задач и поэтому, как правило, недопустим. Maple-язык программирования имеет встроенные средства для исключения побочных эффектов. Встречая такие операции присваивания, Maple-язык корректирует текст процедуры и вставляет в нее объявление переменных локальными с помощью ключевого слова local и выдает предупреждающую надпись о подобном применении:

> т:=0;

т := О

> modc:=proc(z) > m:=evalf(sqrt(Re(z)л2+lm(z)A2)):

> RETURN(m) > end;

Warning, 'm' is implicitly declared local

mode := proc(z) local m:

m := e\/a«(sqrt(Re{z^2 + \m(z^2)); RETURN(m) end

> modc(3.+l*4.);

5.000000000 > m;

9.8.9. Объявления переменных глобальными с помощью оператора global

Говорят, запретный плод сладок! Что бы ни говорили о нежелательности работы с глобальными переменными, бывает, что их применение желательно или даже необходимо. Чтобы сделать переменные внутри процедуры глобальными, достаточно объявить их с помощью ключевого слова global, после которого указывается перечисление переменных.

Следующий пример поясняет применение оператора global в процедуре:

>а:=1;Ь:=1;

а := 1 b := 1

> fg:=proc(x,y) > global a,b;

> a:=x"2\ b:=yл2;

> RETURN(sqrt(a+b));

>end;

fg := proc(x, y) global a, b; a := ^2; b := y"2: RETURN(sqrt(a + b)) end;

> fg(3.4);

5 >a;

9 >b;

Следует отметить, что нельзя делать глобальными переменные, указанные в списке параметров процедуры, поскольку они уже фактически объявлены локальными. Такая попытка приведет к появлению сообщения об ошибке следующего вида «Error, argument and global 'x' have the same name». При этом соответствующие переменные останутся локальными.

9.8.10. Функция вывода сообщений об ошибках ERROR

При профессиональной подготовке процедур пользователь должен предусмотреть поведение процедуры при возможных ошибках. Для этого обычно используются различные функции оценки и тестирования. При выявлении ими ошибки обычно предусматривается вывод соответствующего сообщения. Для этого используется функция ERROR:

ERROR(expr_l, expr_2, ...),

где expr_l, ... — ряд выражении (возможно, пустой). Наиболее часто ERROR выводит просто строковое сообщение об ошибке, например, ERRORCstrings'). Полное сообщение об ошибке имеет вид:

Error, (in name) string,...

Приведем пример процедуры, в которой предусмотрен вывод сообщения об ошибке при задании переменной х<0:

> logbase := proc (x,b::integer) if x<0 then ERRORfinvalid x', x) else evalf(ln(x)/ln(b)) fi end:

>logbase(100,2);

6.643856189

> logbase(-100,2);

Error, (in logbase) invalid x, -100

>logbase(100,1.5);

Error, logbase expects its 2nd argument, b, to be of type integer, but received 1.5

Эта процедура вычисляет логарифм числа х основанию b с выводом результата в форме десятичного числа с плавающей точкой. Поскольку отрицательные числа логарифмов не имеют, сообщение об ошибке появляется при х<0. Обратите внимание также и на другое сообщение об ошибке при задании Ь=1.5. В данном

Типовые средства программирования 151

случае это сообщение обусловлено тем, что параметру b присвоен тип целого числа.

9.8.11. Опции (ключи) в процедурах

В объявление процедуры можно включить опции, вводимые словом options <nseq>

Иногда опции называют расширяющими ключами. Предусмотрены следующие опции:

remember — определяет таблицу памяти для процедуры;

builtin — определяет функцию как встроенную;

system — определяет процедуру как системную;

operator — объявляет процедуру — функциональный оператор;

arrow — определят процедуру в нотации ->;

angle — определяет процедуру в нотации <... ...>;

trace — задает трассировку процедуры;

package — определяет процедуру для пакета расширения;

Ключ remember

Ключ remember обеспечивает занесение результатов обращении к процедуре в таблицу памяти. Функция ор позволяет вывести таблицу:

> f:=proc(x) options remember; x'^S end:

>f(2);

>f(3);

> op(4,eval(f));

table([

3=27

2=8

])

Ключ remember особенно полезен в реализации итерационных процедур. К примеру, в приведенной ниже процедуре вычисления п-го Фибоначчи время вычисления растет пропорционально квадрату п:

> f:=proc(n) if n<2 then n else f(n-1 )+f(n-2) fi end:

>f(30);

832040

Вычисление f(30) по этой процедуре на ПК с процессором Pentium 200 ММХ занимает около минуты.

Стоит добавить в процедуру опцию remember, как время вычислений начнет расти пропорционально n:

> fe:=proc(n) options remember; if n<2 then n else f(n-1 )+f(n-2) fi end:

> fe(30);

832040

> time(fe(20));

О > time(fe(30));

, О

При этом повторное вычисление fe(30) происходит практически мгновенно, так как все промежуточные результаты в первом случае вычисляются заново, а во втором они берутся из таблицы. Однако это справедливо лишь тогда, когда к процедуре было хотя бы однократное обращение. Надо отметить, что данные процедуры являются рекурсивными, т.е. в их теле имеется обращение к самой себе.

Ключ builtin

Ключ build придает процедуре статус встроенной. Он должен использоваться всегда первым. С помощью функции eval(name) можно проверить, является ли функция с именем name встроенной:

> eval(type);

ргос() option builtin; 161 end > eval(print);

proc() option builtin: 139 end

Числа в теле процедур указывают системные номера функций.

Ключ system

Этот ключ придает процедуре статус системной. У таких процедур таблица памяти может быть удалена. У обычных процедур таблица памяти не удаляется и входит в так называемый «мусорный ящик» (garbage collector).

Ключ operator, angle

Ключ operator задает процедуре статус оператора в нотации угловых скобок. Пример применения ключа дан ниже:

> о:=ргос(х,у) option operator angle;x-sqrt(y) end:

> o(4,2.);

2.585786438

Напоминаем, что эта нотация возможна только в реализации Maple V R3.

Ключ operator, arrow

Этот ключ задает процедуре статус оператора в нотации стрелки (—>). Это достаточно пояснить следующими примерами:

> o:=proc(x,y) option operator,arrow:x-sqrt(y) end;

о := (х, у) -> х - sqrt(y) > о(4,2.);

2.585786438

Ключ trace

Ключ trace задаёт в процедуре вывод отладочной информации:

> о:=ргос(х,у) option trace; x-sqrt(y) end;

о := ргос(х, у) option trace; х - sqrt(y) end

> 0(4,2.);

{-> enter o, args = 4, 2.

2.585786438

<- exit o (now at top level) = 2.585786438} 2.585786438

Ключ package

Ключ package используется для придания процедуре статуса пакетной процедуры. О подготовке таких процедур мы расскажем ниже.

Ключ copyright

Этот ключ защищает процедуру от просмотра. Это поясняют следующие два примера:

> o:=proc(x,y) x-sqrt(y) end;

о := ргос(х, у) х - sqrt(y) end > о(4,2.);

2.585786438 > eval(o);

proc(x, у) х - sqrt(y) end > oo:=proc(x,y) option Copyright;x-sqrt(y) end;

oo := proc(x, y)... end > eval(oo);

ргос(х, у)... end

Нетрудно заметить, что во втором примере тело процедуры уже не просматривается. Для отмены защиты от просмотра можно использовать оператор interfa-ce(verboseproc=2).

9.8.12. Общая форма задания процедуры

Выше мы рассмотрели основные частные формы задания процедур. Все они могут быть объединены в общую форму задания процедуры:

name:=proc(<argseq>) — объявление процедуры;

local<nseq>; — объявление локальных переменных;

global<nseq>; — объявление глобальных переменных;

options<nseq>; — объявление опций (расширяющих ключей);

description<stringseq>; — объявление комментариев:

<stateq> — выражения — тело процедуры;

end; (или end:) — объявление конца процедуры.

Эта форма охватывает все описанные выше частные формы и позволяет готовить самые сложные и надежно работающие процедуры.

9.8.13. Средства контроля и отладки процедур

Большая часть функций и операторов системы Maple V реализована в виде процедур, написанных на Maple-языке программирования. Благодаря возможности их просмотра пользователь получает неисчерпаемый источник примеров

154 Основные понятия входного языка системы Maple V

программирования на этом языке. Кроме того пользователь может создавать свои собственные процедуры.

Для контроля и отладки процедур прежде всего надо уметь вывести их полный список. Для этого служит функция:

print(name);

где name — имя процедуры.

Однако перед тем как использовать эту функцию, надо исполнить команду > lnterface(verboseproc=2,prettyprint=1 .version);

Maple Worksheet Interface, Release 4, IBM INTEL NT, Jan 16 1996

Ее смысл будет пояснен ниже. Пока же отметим, что эта команда обеспечивает полный вывод текста процедур библиотеки. Встроенные в ядро процедуры, написанные не на Maple-языке, в полном тексте не представляются. Поясним это следующими примерами:

> print(evalf);

ргос() option builtin, remember; 89 end

> print(erf);

proc(x)

option

ifnargs о 1 then ERROR('expecting 1 argument, got '.nargs)

elif type(x, 'complex(float)') then evalf('erf(x))

elif type(x, 'complex(numeric)') then if csgn(x) = -1 then -erf(-x) else 'erf(x) fi

eliftype(x, "") and type(op(1, x), 'complex(numeric)') and

csgn(op(1, x)) = -1 then -erf(-x)

elif type(x, '+') and traperror(sign(x)) = -1 then -erf(-x)

else erf(x) := 'erf(x)

fi end >

Здесь вначале выполнен вывод сокращенного листинга встроенной в ядро процедуры evalf, а затем выведен полный листинг процедуры вычисления функции ошибок erf. Эта функция имеет довольно короткую процедуру — многие важные функции и операторы задаются гораздо более сложными и большими процедурами.

Но вернемся к функции interface. Эта функция служит для управления выводом и задается в виде:

interface( argi, arg2, ... ) где аргументы задаются равенствами вида name=value и словами-указателями:

ansi echo errorbreak indentamount labelling labelwidth patchlevel plotdevice plotoptions plotoutput postplot preplot prettyprint prompt quiet screenheight screenwidth showassumed terminal verboseproc version warnlevel

Типовые средства программирования 155

К сожалению, объем книги не позволяет остановиться на всех вариантах использования этой очень мощной функции — тем более что в ней может использоваться множество аргументов. Мы рассмотрим только некоторые, наиболее важные возможности.

Указание verboseproc=n задает степень детальности вывода листинга процедур. При п=0 текст не выводится, при n=l выводится текст только заданных пользователем процедур, а при n=2 — всех процедур на Maple-языке. Пример этого был дан выше. Указание prettyprint=0 или I управляет выводом стандартных сообщений. Указание plotdevice=string управляет выводом графики, например, plotdevice =gif указывает на то, что запись графиков в виде файлов будет происходить в формате .gif.

Одним из основных средств отладки процедур является функция трассировки trace(name). Детальность ее работы задается системной переменной printlevel (уровень вывода). При printlevel:=n (значение n=l по умолчанию) результат выводится только непосредственно исполняемой функции или оператора. Для вывода информации о выполнении k-ro уровня вложенности надо использовать значение этой переменной от 5*k до 5*(k+l). Так, при п от I до 5 выводятся результаты трассировки первого уровня, при п от 6 до 10 — второго и т.д. Максимальное значение п=100 обеспечивает трассировку по всем уровням вложенности процедуры name.

Следующий пример показывает осуществление трассировки для функции int(x'n,x):

> printlevel:=5;

printlevel := 5 > trace(int);

int > шЦх^п.х);

{-> enter int, args = x'4i, x

_EnvsignumO := _EnvsignumO x := x

indef := true _Envlndefinite := true

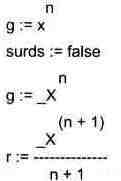
fens := {} expargs := Q Eiaras •= Л

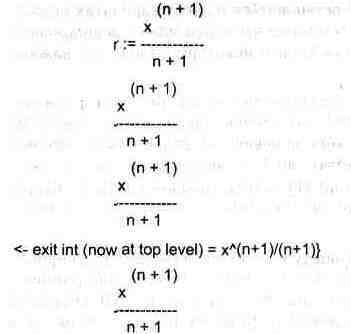
Действие функции трассировки отменяется оператором untrace:

> untrace(int);

int

> intfx^.x);

1/3 х

При отладке алгоритмов выполнения вычислений надо тщательно следить за сообщениями об ошибках. Для этого в Maple предусмотрена функция traceerr и системная переменная lasterr, в которой сохраняется последнее сообщение об ошибке. При каждом обращении к tracerr переменная lasterr очищается:

>2/0;

Error, division by zero

>2/4;

1/2

> lasterror;

division by zero

> traperror(3/4);

3/4

> lasterror;

lasterror

> traperror(5/0);

Error, division by zero > lasterror;

division by zero

Этот пример показывает, как может быть проведено отслеживание ошибок в ходе вычислений. Вообще говоря, пользователь редко привлекает описанные средства, поскольку проще отладить вычислительный алгоритм прежде, чем на его основе будет составлена процедура. При правильном построении процедур ошибочные ситуации заведомо предусматриваются и должным образом обрабатываются.

Типовые средства программирования 157 9.8.14. Работа с отладчиком программ (debugging)

В большинстве случаев составители программ (процедур) редко прибегают к пошаговой их отладке. Средства общей диагностики Maple V развиты настолько хорошо, что позволяют выявлять грубые ошибки в процедурах при их общем выполнении. Иногда, правда, для этого приходится неоднократно «прогонять» процедуру, пока она не начнет работать, как задумано. Тем не менее для отладки процедур служит специальный интерактивный отладчик — debugger. Опишем, как его запустить и как с ним работать.

Допустим, мы составили некоторую процедуру demo, вычисляющую сумму квадратов чисел (1"2+2'2+...+п"2):

> demo:=proc(n::integer) local y,i: y:=0: for i to n do у:=у+^2 od end;

demo := proc(n::integer) localy, i;

у := 0; for i to n do у := у + ^2 od end

> demo(3);

Чтобы включить отладчик в работу, надо исполнить команду stopat:

> stopat(demo);

[demo]

> demo(3);

demo:

1*y:=0;

DBG> next

Признаком, указывающим на работу отладчика, является изменение приглашения к вводу со знака > на DBG> (как нетрудно догадаться, DBG означает debugger).

Теперь, подавая команды next (следующий), step (шаг) и stop (остановка), можно проследить выполнение процедуры:

Ок demo:

2 for i to n do

od DBG> step 0 demo:

3 у := y+\"2 DBG> step 1 demo:

3 у := у+^2 DBG> step 5 demo:

3 у := y+i^ DBG> step

В последнем случае процедура по шагам дошла до конца вычислений, и на этом работа отладчика завершается сама собой.

158 Основные понятия входного языка системы Maple V

Можно также вывести листинг процедуры с помощью команды:

> showstat(demo);

demo := proc(n::integer) localy, i;

1* y:=0;

2 for i to n do

3 у := y+i"2

od end >

Обратите внимание, что в этом листинге строки вычисляемых элементов пронумерованы. Это сделано для облегчения разбора работы процедуры.

В общем случае отладчик включается при выполнении команд stopat, stopwhen или stoperr. Если используется команда stopat, то вывод на экран соответствует исполнению последней выполненной команды. Для отмены этой команды используется команда unstopat.

Команда stopwhen позволяет установить точку наблюдения за указанной после нее переменной. Отменить ее можно командой unstopwhen. Команда stoperror позволяет задать остановку при появлении определенной ошибки. Для отмены этой команды используется команда unstoperror.

Команда cont используется для продолжения работы до следующей точки прерывания, установленной указанными выше командами, или до конца процедуры. Для прерывания отладки можно использовать команду quit. После команды stop можно вычислить любое Maple-выражение.

В действительности команд отладчика намного больше и их функции более развиты, чем это описано выше. Пользователи, заинтересованные в серьезной работе с отладчиком (скорее всего их немного), могут просмотреть его подробное описание. Для этого в разделе справочной системы Context (справка по контексту) найдите раздел Programming (Программирование) и в нем раздел Debugging (Отладка).

9.9. Операции ввода и вывода 9.9.1. Считывание и запись программных модулей

В главе 2 рассматривалась работа с файлами документов. Вводимые в текущий документ программные модули хранятся вместе с ним. Так что при отказе от загрузки какого-либо документа все его программные блоки не могут использоваться в других документах. Кроме того, порою неудобно загружать объемный документ ради использования одного или нескольких модулей, например, процедур. Поэтому в Maple V введены средства, позволяющие записывать нужные модули (в том числе результаты вычислений) на магнитные диски ПК и считывать их в случае необходимости.

Для записи на магнитный диск используется оператор save:

save filename — запись всех определений текущего файла под именем filename;

save name_l, name_2, ..., name_k, filename — запись избранных модулей с именами name_l, name_2,..., name_k под именем filename.

Операции ввода и вывода 159

Считывание имеющегося на диске файла с именем filename осуществляется оператором read:

read <filename>

При считывании все имеющиеся в файле определения становятся доступными для рабочих документов Maple V. При записи файлов отдельных определений используется специальный внутренний Maple-формат файлов. Для загрузки файлов типа *.т из стандартной библиотеки используется функция readlib. А для записи файлов в качестве библиотечных достаточно в имени filename оператора save указать расширение .т. Разумеется, можно считывать такие файлы и оператором read, указав в имени файла расширение .т:

> save my_proc,'my_lib.m': # запись файла ту_ргос и библиотечного файла myJib.m;

> load 'myJib.m': ^считывание библиотечного файла myJib.m.

9.9.2. Создание своей библиотеки процедур

Если приведенные выше примеры составления процедур кажутся вам простыми, значит, вы неплохо знаете программирование и, скорее всего, уже имеете несколько полезных процедур, которые вы хотели бы сохранить — если и не потомков, то хотя бы для своей повседневной работы. Сделать это в Maple V довольно просто.

Прежде всего надо определить имя своей библиотеки, например mylib, и создать на диске под нее каталог (папку) с заданным именем. Процедуры в Maple V ассоциируются с таблицами. Поэтому вначале надо задать таблицу 0 — пустышку под будущие процедуры:

> mylib:=table();

mylib := table([

]) Теперь надо ввести свои библиотечные процедуры. Они задаются с двойным именем:

вначале указывается имя библиотеки, а затем в квадратных скобках — имя процедуры. Для примера зададим три простые процедуры с именами fl, f2 и f3:

> mylib[f1]:=proc(x::anything) sin(x)+cos(x) end:

> mylib[f2]:=proc(x::anything) smfx^+costx)^ end:

> mylib[f3]:=proc(x::anything) ifx=0 then 1 else sin(x)/x fi end:

Рекомендуется тщательно проверить работу процедур, прежде чем записывать их на диск. Ограничимся, скажем, такими контрольными примерами:

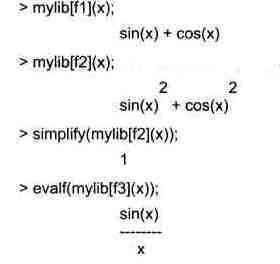
> evalf(mylib[f3](0));

>evalf(mylib[f3](1));

.8414709848

С помощью функции with можно убедиться, что библиотека mylib действительно

содержит только что введенные в нее процедуры. Их список должен появиться при обращении к with(mylib):

> with(mylib);

[f1.f2.f3]

Теперь надо записать эту библиотеку под своим именем на диск с помощью команды save:

> save'c:/mylib.m';

Обратите особое внимание на правильное задание полного имени файла. Обычно применяемый для указания пути знак \ в строках Maple-языка используется как знак продолжения строки. Поэтому надо использовать либо двойной знак \\, либо знак /. В нашем примере файл записан в корневую директорию диска С. Если вы решили поместить библиотечный файл в другую директорию (например, в библиотеку, уже имеющуюся в составе системы), укажите полный путь вашего файла и убедитесь в том, что указанная вами директория в самом деле существует. Создайте ее, если директории нет.

Затем надо убедиться в том, что библиотечный файл записан, и считать его. Для этого вначале следует командой restart устранить ранее введенные определения процедур:

> restart;

С помощью команды with можно убедиться, что этих определений уже нет:

> with(mylib);

Error, (in with) undefined package, mylib

После этого командой read надо загрузить библиотечный файл:

> read'c:/mylib.m';

Имя файла надо вводить по правилам, указанным для команды save. Если все выполнено пунктуально, команда with должна показать наличие в вашей библиотеке списка процедур fl, f2 и f3:

> with(mylib);

[f1.f2.f3]

И, наконец, можно опробовать вновь работу процедур, которые теперь введены из загруженной библиотеки:

>f1(x);

sin(x) + cos(x)

> simplify(f2(y));

> t3(0);

>f3(1.);

.8414709848

Описанный выше способ создания своей библиотеки вполне устроит большинство пользователей. Однако есть более сложный и более, продвинутый способ ввода своей библиотеки в состав уже имеющейся. Для этого Maple V имеет следующие операции записи в библиотеку процедур sq, s2,... и считывания их из файлов Kiel,

file2,..:

savelib(sl, s2, ...., sn, filename) readlib(f, filel, file2, ...)

С помощью специального оператора makehelp можно задать стандартное справочное описание новых процедур:

makehelp(n,f,b),

где: п — название темы, f— имя текстового файла, содержащего текст справки (готовится как документ Maple) и b — имя библиотеки. Системная переменная libname хранит имя директории библиотечных файлов. Для регистрации созданной справки по вашей библиотеке надо исполнить команду вида:

libname:=libname, '/mylib';

С деталями применения этих операторов можно ознакомиться в справочной системе.

К созданию своих библиотечных процедур надо относиться достаточно осторожно — их применение лишает ваши Maple-программы совместимости со стандартной версией Maple V. Если вы используете одну-две любимые процедуры, проще поместить их в те документы, в которых они действительно нужны. Иначе вы будете вынуждены к каждой своей программе прикладывать еще и свою библиотеку процедур. Она нередко оказывается большей по размеру, чем файл самого документа. Не всегда практично цеплять маленький файл документа к большой библиотеке, большинство процедур которой скорее всего для данного документа попросту не нужно. Особенно рискованно изменять стандартную библиотеку Maple V.

Впрочем, идти на это или нет — дело каждого пользователя. Разумеется, если вы готовы создать серьезную библиотеку своих процедур, то ее надо записать и тщательно хранить. С Maple V поставляется множество библиотек полезных процедур, составленных пользователями со всего мира, так что и вы можете пополнить ее своими творениями (глава 14).

9.9.3. Запись и считывание данных

Обширные возможности Maple V по математической обработке данных делают привлекательным применение этой системы для автоматической обработки данных, поступающих от каких-либо экспериментальных (например, физических установок). Для этого установки снабжаются интерфейсными платами, например, аналогово-цифровыми преобразователями и необходимым программным обеспечением. Возможна и передача полученных Maple V данных в экспериментальные установки.

Обмен информацией между Maple V и внешней средой (к ней, кстати, относятся и другие программы) чаще всего осуществляется через файлы текстового форма-

162 Основные понятия входного языка системы Maple V

та, поскольку именно с такими файлами работают практически все программные средства. Для записи данных в файл служит оператор

writedata[APPEND](fileID, data) writedata[APPEND](fileID, data, format) writedata[APPEND](fileID, data, format, default)

Здесь fileID — имя или дескриптор файла данных, data — список, вектор или матрица данных, format — спецификация формата данных (integer, float или string), default — процедура, задающая запись нечисловых данных, например:

writedata(F,A,float,proc(i,x) iprinti(f,'CMPLX(%g,%g)',Re(x),Im(x)) end);.

Необязательный указатель APPEND используется, если данные должны дописываться в уже созданный файл.

Считывание из полученного файла с именем filename обеспечивает функция

readdata(fileID, n) readdata(fileID, format, n) readdata(fileID, format)

Здесь n — целое положительное число, задающее число считываемых столбцов. Ниже представлены примеры этих операций:

> В := аггау( [[1.5,2.2,3.4],[2.7,3.4,5.6],[1.8,3.1,6.7]]);

[1.5 2.2 3.4]

[ 1 [2.7 3.4 5.6]

[ 1 [1.8 3.1 6.7]

> writedata('C:\\mydata.txt',B);

> E:=readdata('C:\\mydata.txt',3);

Е := [[1.5, 2.2, 3.4], [2.7, 3.4, 5.6], [1.8, 3.1, 6.7]] Maple V также имеет типичные файловые операции:

writeto — запись в файл;

appendto — дозапись в файл;

open — открытие файла;

close — закрытие файла;

write — запись в открытый файл;

save — запись выражений в файл;

read — считывание из файла.

Их осуществление, однако, зависит от платформы, на которой установлена система, и от ее настройки. Ряд других файловых операций, в частности, с буферизованными файлами вы найдете в Приложении 1 и, разумеется, в справочной системе Maple V.

9.10. Вывод в специальных форматах 9.10.1. Вывод в формате LaTeX

Maple V имеет ряд средств для общения с другими признанными математическими программами. Часть из них, в основном относящаяся к обмену через файлы.

Вывод в специальных форматах 163

была уже описана. Однако Maple V способна генерировать коды для прямого их включения в такие программы.

Для подготовки математических статей и книг широкое распространение получили редакторы класса ТеХ и LaT'eX. Для подготовки выражений или файлов в их формате служит функция

latex(expr, filename)

Параметр filename не обязателен, если достаточно получить нужное выражение в ячейке вывода Maple V:

> latexfa'x^+b'x+c);

a{x}A{2}+bx+c

> latex(diff(xлn,x$2));

{\frac {{хПпКп}^}}^}^}}}-^ {{хИпИйх}^}}}

9.10.2. Генерация кодов на языке Фортран

Язык Фортран вот уже десятилетия используется для программирования вычислительных задач. Накоплены обширные библиотеки решения таких задач на Фортране. Почитателей этого языка Maple V порадует тем, что он позволяет готовить коды для программ на Фортране. Для этого используется функция:

fortran(expr,filename=str,optomized)

Два последних параметра необязательны при выводе выражения ехрг в форме, присущей языку Фортран:

> fortrar^a'x'^+b'x+c);

t0 = a*x"2+b*x+c

> fortrar^dif^n^));

t0 = x-n'n'^/x^-x-n'n/x-^

Опция optimize позволяет генерировать оптимизированные коды:

>fortran(diff(xлn,x$2),optimized);

t1 = х**п

t2 = п"2

t4 = х-2

t5= 1/t4

t9= 11 •{2*15-11 •n't5

При этом вычислительный процесс строится так, чтобы минимизировать число арифметических операций.

9.10.3. Генерация кодов на языке С

Язык С (Си) также широко используется для решения вычислительных задач. Достаточно отметить, что сама система Maple V создана на языке С.

Для генерации кодов на языке С вначале надо подключить библиотечную функцию С:

> readlib(C);

ргос()... end

Для генерации кодов на языке С служит функция:

C(expr,folename=str, optimized)

164 Основные понятия входного языка системы Maple V

Эта функция используется по аналогии с функцией fortran, что и показывают приведенные ниже примеры:

> C(diff(xлn,x$2));

t0 = pow()(.,n)'r}'n/(x*^)-pow(x,f\)'r\i(x*x);

> C(diff(x'^n,x$2),optimized);

t1 = pow(x,n);

t2 = п*п;

t4 = х*х;

t5=1/t4;

19=11*12'{5-1ГпЧ5;

Обширные возможности по преобразованию выражении в различные формы представляет функция convert. А функция interface позволяет управлять выводом. К сожалению, объем книги не позволяет рассмотреть все многочисленные варианты применения этих функций.

9.11. Дополнительные возможности Maple-языка 9.11.1. Переназначение определений

В большинстве случаев Maple-язык использует достаточно длинные идентификаторы для своих определений, например, функций. Однако с помощью функции alias можно изменить любое определение на другое, если оно кажется пользователю более удобным.

Функция alias записывается в виде:

alias(el, e2, ..., eN), где е1, e2, ..., eN — ноль или более равенств.

Эта функция возвращает список переназначений и осуществляет сами переназначения.

Например, для замены имени функции BesselJ на более короткое имя BJ достаточно параметром функции alias записать BJ=BesselJ:

> alias(BJ=BesselJ);

I.BJ >BesselJ(0,1);

BJ(0, 1) > BesselJ(0,1.);

.7651976866 >BJ(0,1);

BJ(0, 1)

>BJ(0,1.);

.7651976866

Можно также переназначить функцию пользователя:

> alias(Fx=int(Func(x),x));

1. BJ, Fx

> int(Fx,x);

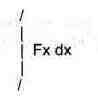
> has(Fx(x),x);

true

Для отмены переназначения, например, BJ, используется та же функция alias с повтором переназначения:

> alias(BJ=BJ);

I.Fx >BJ(0,1.);

BJ(0,1.)

Обратите внимание на то, что BJ исчезло из списка переназначений и функция BJ(0,1.) уже не вычисляется 0, поскольку ее уже нет.

9.11.2. Макросы

Макрос — это короткая запись длинных определений. По сравнению с переназначениями макросы более гибки и могут использоваться для сокращения операций загрузки новых определений из библиотеки и пакетов расширения.

macro(el, е2, .... en)

где el,e2,...,en — ноль или более равенств.

В следующем примере функция numbperm с помощью макроса заменена на пр:

> with(combinat):numbperm([1,2,3,4]);

24 > macro(np=numbperm(V));

>V:=[1,2,3,4];

V :=[-!, 2, 3,4] > np(V);

С помощью функции macro можно задавать новые типы данных. Например, ниже показано задание такого типа данных, как запись:

> macro(one=1 ,two=2,three=3,four=4);

>z[1];

> z[one];

а > z[one]+z[two]'z[four];

a+bd

Макросы могут быть использованы для конструирования выражений из их макроопределений.

9.11.3. Внешние вызовы

Maple V имеет команду system(string), с помощью которой можно исполнить любую команду MS-DOS, записанную в виде строки string. Например, для обзора директории UT диска С достаточно задать команду

>system('dirC:\UT');

На экране кратковременно появится окно MD-DOS с перечнем файлов директории UT диска С. Это окно показано на рис. 9.4.

Рис. 9.4. Результат выполнения команды systemCdir C:\UT').

На практике при работе в операционной системе Windows эта возможность практически бесполезна, поскольку данное окно, «прокрутив» файлы в указанной директории, тут же исчезает с экрана. Разумеется, есть операции, которые можно таким образом выполнить командами MS-DOS, например, скопировать файл или изменить его имя. Но только дело в том, что Windows имеет для всего этого куда более простые и удобные средства.

Внешние вызовы командой system куда более полезны для MS-DOS—реализации Maple V, которые кое-где используются и по сей день. Но, поскольку данная книга посвящена самым современным реализациям системы Maple V под Windows, оолее подробное рассмотрение операций внешних вызовов не имеет особого

смысла.

Вычисление сумм рядов

167

Глава 10. Операции и функции

математического анализа

10.1. Вычисление сумм рядов

Применение систем символьной математики особенно эффектно при решении задач математического анализа. Начнем рассмотрение таких операций с вычисления сумм. Вычисление суммы членов некоторой последовательности f(k) при изменении целочисленного индекса k от значения m до значения п с шагом +1, т.е. выражения

является достаточно распространенной операцией математического анализа. Для вычисляемой и инертной форм вычисления сумм служат следующие функции:

sum(f,k) suni(f,k=m..n) sum(f,k=alpha) Sum(f,k) Sum(t,k=m..n) Sum(f,k=alpha)

где: f — функция, задающая члены суммируемого ряда, k — индекс суммирования, тип — целочисленные пределы изменения k, alpha — RootOf-выражение. Значение п может приниматься бесконечным, тогда для п используется константа infinity.

	Фиксатор выражения, предотвращающий вывод результата вычисления в ячейку вывода.
,	Фиксатор выражения, дающий вывод результата вычисления в ячейку вывода.
#	Указатель программного комментария.
•	Ограничитель строки (например, 'string').

:=»	Оператор присваивания (например, х:=5).
,,	Пустой оператор.
	Указатель типа переменной (например, n::integer или z::complex).

eval(array)	Возвращает содержимое массива array.
evalf(expr, n)	Вычисляет ехрг и возвращает вычисленное значение в форме числа с плавающей точкой, имеющего n цифр после десятичной точки.
evalhf(expr)	Вычисляет ехрг и возвращает вычисленное значение с точностью, присущей данной компьютерной системе.
evalf(int(f, x=a..b))	Оценивает и возвращает значение определенного интеграла int(f,x=a..b).
evalf(Int(f, x=a..b))	Оценивает и возвращает значение определенного интеграла, заданного инертной функцией Int(f,x=a..b).
evalf(Int(f, x=a..b. digits, flag))	Аналогично предыдущему, но возвращает значение интеграла с заданным числом цифр после десятичной точки digits и со спецификацией метода вычислений flag.
evalm(mexpr)	Вычисляет значение матричного выражения mexpr и возвращает его.
evalb(bexpr)	Вычисляет и возвращает значения логических условий.
evalc(cexpr)	Вычисляет значение комплексного выражения.
evalr(expr, ampi)	Оценивает и возвращает значения интервальных выражений (функция должна вызываться из библиотеки).
shake(expr, ampi)	Вычисляет интервальное выражение.

sin	cos	tan	csc	sec	cot
sinh	cosh	tanh	csch	sech	coth
arcsin	arccos	arctan	arccsc	arcsec	arccot
arcsinh	arccosh	arctanh	arccsch	arcsech	arccoth
exp	In	sqrt		abs	conjugate
polar	argument	signum	csgn	Re	Im
Ei	LambertW	dilog	surd

binary	Бинарные операторы (двумя операндами).
unary	Унарные операторы (с одним операндом).
nullary	Нульарные операторы (без операнда — это одна, две и три пары кавычек.
precedence	Операторы старшинства (включая логические операторы).
functional	Функциональные операторы.

+	Сложение.	-	Вычитание.
*	Умножение.	/	Деление.
** или	Возведение в степень.	mod	Вычисление модуля.
$	Оператор последовательности.	,	Разделительная точка.
@	Оператор композиции.	@@	Повторение композиции.
	Задание области (интервала).	:=	Присваивание.
&*	Некоммутативное умножение.	»	Разделитель выражений.
\и.	Конкатенация (объединение).	&string	Нейтральный оператор.

union	Включает первый операнд (множество) во второй.
intersect	Создает множество, содержащее общие для операндов элементы.
minus	Исключает из первого оператора элементы второго.

+	Унарный плюс (префикс).	-	Унарный минус (префикс).
!	Факториал (постфиксный).		Десятичная точка (префикс или постфикс).
$	Последовательность (префикс).	not	логическое отрицание (префикс).
%	Метка (префикс).

<	Менее чем.	<=	Менее чем или равно.
>	Более чем.	>=	Более чем или равно.
=	Равно.	о	Не равно.
and	Логическое И.	or	Логическое ИЛИ.

Нотация	Запись оператора
"arrow" (стрелочная)	vars -> result
"angle bracket" (в угловых скобках)	<result ¦ vars>

factorial	Функция вычисления факториала (альтернатива — оператор !).
iquo(a,b)	Частное для а/Ь.

irem(a,b)	Остаток для a/b.
igcd(a b)	Наибольший общин делитель.
lcm(a.b)	Наименьшее общее кратное.

sin	Синус.	CSC	Косеканс.
sec	Секанс.	tan	Тангенс.
cos	Косинус.	cot	Котангенс.

sinh	Гиперболический синус.	seen	Гиперболический секанс.
cosh	Гиперболический косинус.	csch	Гиперболический косеканс.
tanh	Гиперболический тангенс.	coth	Гиперболический котангенс.

arcsinh	Гиперболический арксинус.	arcsech	Гиперболический арксеканс.
arccosh	Гиперболический арккосинус.	arccsch	Гиперболический арккосеканс. ,
arctanh	Гиперболический арктангенс.	arccoth	Гиперболический арккотангенс.

ехр	Экспоненциальная функция.
iloglO	Целочисленный логарифм по основанию 10.

ilog	Целочисленный логарифм (библиотечная функция).
In	Натуральный логарифм.
log	Логарифм по заданному основанию (библиотечная функция).
loglO	Логарифм по основанию 10.
sqrt	Квадратный корень.

ceil	Наименьшее целое, большее или равное х.
floor	Наибольшее целое, меньшее или равное х.
frac	Дробная часть числа.
trunc	Меньшее целое, округленное в направлении х=0.
round	Округленное значение числа.
signum	Функция знака (-1 при х<0, 0 при х=0 и +1 при х>0).

abs	Абсолютное значение действительного или комплексного числа.
argument	Аргумент комплексного числа.
conjugate	Комплексно-сопряженное число.
Im	Мнимая часть комплексного числа.
Re	Действительная часть комплексного числа.
polar	Полярное представление комплексного числа (библиотечная функция).
max	Максимальный по значению элемент списка.
min	Минимальный по значению элемент списка. '!Q

AiryAi (Bi)	Функции Эири.
AngerJ	Функция Ангера.
bernoulli	Числа и полиномы Бернулли.
Bessell (J, K, Y)	Функции Бесселя разного рода.
Beta	Бета-функция.
binomial	Биноминальные коэффициенты.
Chi	Интегральный гиперболический косинус.
Ci	Интегральный косинус.
csgn	Комплексная сигнум-функция.
dilog	Дилогарифм.
Dirac	Дельта-функция Дирака. . . ,
Ei	Экспоненциальный интеграл.
EllipticCE (CK, CPi, E, F, K, Modulus, Nome, Pi)	Эллиптические интегралы.
erf	Функция ошибок.
erfc	Дополнительная функция ошибок.
euler	Числа и полиномы Эйлера.
FresneIC (f,g,S)	Интегралы Френеля.

GAMMA	Гамма-функция.
GaussAGM	Гаусса арифметико-геометрическое среднее.
HankelHl (H2)	Функции Ханкеля.
harmonic	Частичная сумма серии гармоник.
Heaviside	Функция Хевисайда.
JacobiAM (CN. CD, CS, DN,DC,DS, NC, ND,NS,SC, SD, SN)	Эллиптические функции Якоби.
JacobiThetal (2, 3, 4)	Дзета-функции Якоби.
JacobiZeta	Зет-Функция Якоби.
KelvinBer (Bei, Her, Hei, Ker, Kei)	Функции Кельвина.
Li	Логарифмический интеграл.
InGAMMA	Логарифмическая Гамма-функция.
MeijerG	Меиера G-функция.
pochhammer	Символ Постмайера.
polylog	Полилогарифмическая функция.
Psi	Полигама-функция.
Shi	Синусный гиперболический интеграл.
Si	Интегральный синус.
Ssi	Синусный интеграл смещения.
StruveH (L)	Функции Струве.
surd	Не главная корневая функция.
LambertW	Ламберта W-функция.
WeberE	Вебера Е-функция.
WeierstrassP	Р-функция Вайерштрассе.
WeierstrassPPrime	Производная Р-функции Вайерштрассе.
WeierstrassZeta	Зета-функция Вайерштрассе.
WeierstrassSigma	Сигма-функция Вайерштрассе.
Zeta	Зета-функция Римана и Гурвица.

lenght(str)	Возвращает число символов в строке str.
substring(str,a..b)	Возвращает подстроку в виде символов от а-го до Ь-го строки str.
cat(strl,str2,...)	Возвращает строку, полученную объединением строк strl, str2,... (альтернатива — оператор конкатенации в виде точки .).
SearchText(s,str)	Дает поиск подстроки s в строке str и при его успехе возвращает номер позиции s в строке str (при отсутствии s в str возвращает 0).